Принятие решений в условиях риска

Если решение принимается в условиях риска, то стоимости альтернативных решений обычно описываются вероятностными распределениями. По этой причине принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат. Такой подход имеет свои недостатки, которые не позволяют использовать его в некоторых ситуациях. Для них разработаны модификации упомянутого критерия.

Критерий ожидаемого значения сводится либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что прибыль (затраты), связанные с каждым альтернативным решением, является случайной величиной. В приведенном ниже примере рассматривается простая ситуация, связанная с принятием решения при наличии конечного числа альтернатив и точных значений матрицы доходов.

Предположим, что вы хотите вложить на фондовой бирже 10000 долл. В акции одной из двух компаний: А или В. Акции компании А являются рискованными, но могут принести 50 % прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиции может обесцениться на 20 %. Компания В обеспечивает безопасность инвестиций с 15 % прибыли в условиях повышения котировок на бирже и только 5 % - в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60 % прогнозируют повышение котировок и с вероятностью 40 % - понижение котировок. В какую компанию следует вложить деньги?

Условия игры задаются в виде матрицы А = (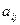), в которой строки соответствуют стратегиям человека, а столбцы - возможным состояниям "природы". В некоторых задачах для состояний "природы" может быть задано распределение вероятностей, в других - оно не­известно. Элемент 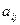равен выигрышу человека, если он использует i-ю стратегию при j-том состоянии "природы". При решении игры часто рассматривают матрицу рисков R = (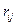). Элемент 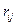равен разности между выигрышем, который получил бы человек, если бы знал состояние природы, и выигрышем, который он получит в тех же условиях, применяя i-ю стратегию, то есть

= -, = .

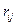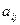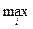
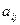Оптимальную стратегию можно получить, используя критери­й ожидаемого значения.

Пусть распределение вероятностей различных состояний "приро­ды" известно p = (p₁,..p_n),

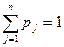. Следовательно, выбирая i-ю стратегию, человек может рассчитывать на средний выигрыш

М_i =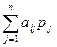(Математическое ожидание).

Критерием принятия решения служит критерий Байеса: наилучшей является стратегия, имеющая максимум математического ожидания выигрыша (минимум математического ожидания риска).

Для сформулированной выше задачи будем иметь:

А =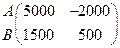

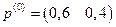
Существуют и другие модификации критерия ожидаемого значения. Например, определение апостериорных вероятностей на основе эксперимента над исследуемой системой или определение полезности реальной стоимости.

Дата добавления: 2014-01-07