Временные характеристики

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ И ЕЕ ЭЛЕМЕНТОВ

ВРЕМЕННЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ

Дифференциальные уравнения являются исчерпывающим математическим описанием САУ. Решения дифференциальных уравнений показывают изменения параметров объекта управления во времени. Однако, на практике получение решений дифференциальных уравнений является не простой задачей. Но, несмотря на это, решения дифференциальных уравнений широко используются как при анализе, так и при синтезе систем. Только для этого рассматриваются решения дифференциальных уравнений при некоторых стандартных (типовых) воздействиях.

Временными характеристиками называются графики решений дифференциальных уравнений при типовых входных воздействиях. В качестве типовых входных воздействий в основном рассматриваются:

- единичное ступенчатое воздействие (единичная ступенчатая функция) 1(t);

- единичное импульсное воздействие d(t).

Единичное ступенчатое воздействие – это функция

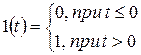, (3.1)

график которой приведен на рис.3.1.

Переходной функцией h(t) называется переходный процесс, вызванный единичным ступенчатым воздействием 1(t) при нулевых начальных условиях, т.е. h(t) характеризует реакцию системы на единичное ступенчатое воздействие, что отражено на рис. 3.2. Если амплитуда ступенчатого воздействия отлична от 1, т.е. 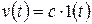, где с – константа, то реакция системы на выходе определяется соотношением:

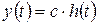. (3.2)

Физическая интерпретация 1 (t) – резкое изменение (скачком) входного воздействия.

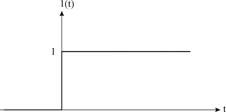
Рис. 3.1. Единичное ступенчатое воздействие

.

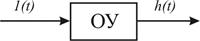
Рис. 3.2. Реакция системы на единичное ступенчатое воздействие

Единичным импульсным воздействием (единичной импульсной функцией) d(t) называется дельта – функцией Дирака, представляющая собой импульс бесконечно большой амплитуды и бесконечно малой длительности:

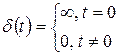, (3.3)

площадь которого равна 1, т.е.

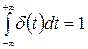. (3.4)

График d(t) представлен на рис. 3.3.

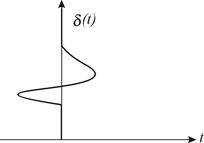
Рис. 3.3. Единичное импульсное воздействие

Импульсной переходной (весовой) функцией w(t) называется переходный процесс, вызванный единичным импульсным воздействием d(t) при нулевых начальных условиях, т.е. w(t) характеризует реакцию системы на входные воздействия типа d - функции, что отражено на рис. 3.4.

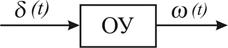
Рис. 3.4.. Реакция системы на единичное импульсное воздействие

Физическая интерпретация d(t) – удар.

Функцию d(t) можно получить дифференцированием функции 1(t), т.е.

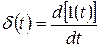. (3.5)

Аналогична связь между h(t) и w(t)

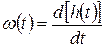. (3.6)

Рассмотрим связь между передаточной, переходной и весовой функциями.

Так как изображение по Лапласу от 1(t)

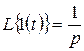, (3.7)

то изображение переходной функции

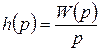, (3.8)

т.е. изображение переходной функции равно передаточной функции, деленной на р. Отсюда имеем, что передаточная функция системы при единичном ступенчатом воздействии 1(t) равна изображению переходной функции, умноженной на р:

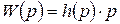. (3.9)

Так как изображение по Лапласу

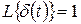, (3.10)

то изображение весовой функции равно передаточной функции, т.е.

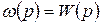. (3.11)

Таким образом: переходная функция является оригиналом передаточной функции, разделенной на р, а весовая функция – оригиналом передаточной функции.

Заключение. Типовые воздействия d(t) и 1(t) с одной стороны описывают поведение системы в экстремальных (тяжелых) условиях, а с другой стороны существенно упрощают возможности получения математических моделей системы (объекта, элемента).

Дата добавления: 2014-01-07