Й учебный вопрос. Определение степени колеблемости

Чтобы определить степень колеблемости результата на практике обычно применяют методы математической статистики, главными инструментами которых являются - дисперсия, среднеквадратичное отклонение, коэффициент вариации.

Дисперсия представляет собой среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых:

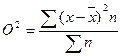где,

х - ожидаемое значение для каждого случая наблюдения;

- средне ожидаемое значение;

n - число случаев наблюдения (частота)

Меру «сжатости» определяет величина, которая в теории веро­ятности носит название «среднеквадратичного отклонения.

Чем меньше величина О, тем больше «сжато» соответствующее распределение вероятностей, и тем менее рискован проект. При этом для нормального распределения вероятность «попадания» в пределы ERR± О составляет 68,26%.

Среднее квадратическое отклонение:

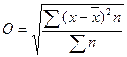
Среднее квадратическое отклонение указывается в тех же единицах, в каких измеряется варьирующий признак.

Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости.

Рассчитаем значение О для рассматриваемых проектов А и В.

Проект А:

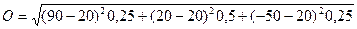= 49,5%

Проект В:

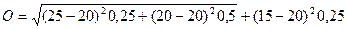= 3,5%

Как видим, для второго проекта с вероятностью 68,26% можно ожидать величину доходности IRR = 20% ± 3,5%, т.е. от 16,5% до 23,5%. Риск здесь минимальный. Проект А гораздо более риско­ванный. С вероятностью 68,26% можно получить доходность от -29,5% до 69,5%. Считается, что среднерискованной операции соответствует значение О около 30%.

В рассмотренном примере распределение вероятностей пред­полагалось известным заранее. Во многих ситуациях бывают дос­тупны лишь данные о том, какой доход приносила некая финан­совая или хозяйственная операция в предыдущие годы.

Например, доступная информация может быть представлена в следующем виде (см. табл.)

таблица 3. Динамика IRR

Год	IRR
	10%
	8%
	О
	15%

В этом случае для расчета среднеквадратичного отклонения О используется такая формула

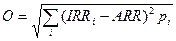
здесь n - число лет, за которые приведены данные,

ARR ­(Average Rate of Return, средняя норма доходности среднее арифметическое всех IRR за n лет - рассчитывается по

формуле:

для нашего примера получаем:

ARR = (10 + 8 + 15)/4 = 8,25%.

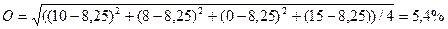
Еще одной величиной, характеризующей степень риска, является коэффициент вариации V.

Коэффициент вариации - отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений:

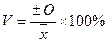
Коэффициент вариации выражает количество риска на единицу доходности И чем выше V, тем выше степень риска.

Коэффициент вариации - относительная величина. Поэтому на его размер не оказывает влияние абсолютные значения изучаемого показателя. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения.

Он изменяется от 0 до 100 %.

Чем больше коэффициент, тем сильнее колеблемость; чем ниже коэффициент, тем меньше размер относительного риска.

Установлена следующая качественная оценка различных значений

коэффициента вариации:

· до 10 % - слабая колеблемость;

· 10- 25 % - умеренная колеблемость;

· свыше 25 % - высокая колеблемость.

В рассмотренном чуть раньше примере для проектов А и В ко­эффициенты вариации равны соответственно:

V _А = 49,5/20 = 2,475;

V _B= 3,5/20 = 0,175.

В данной ситуации найденные коэффициенты уже не добавля­ют существенной информации и могут служить лишь для оценки того, во сколько раз один проект рискованнее другого: 2,475/ 0,175 = 14. Проект А в 14 раз рискованнее проекта В.

Коэффициент вариации необходимо знать в случае, когда тре­буется сравнить финансовые операции с различными ожидаемы­ми нормами доходности ERR.

Пусть для проектов С и D распределение вероятностей задает­ся следующей таблицей

Таблица Распределение вероятностей для проектов С И D

Состояние экономики	Вероятность данного состояния	Проект А; IRR	Проект В, IRR
Подъем	P1 = 0,2	30%	115%
Норма	Р2 = 0,6	20%	80%
Спад	Р3 = 0,2	10%	45%

Рассчитаем для обоих проектов ERR, О и V. По формуле получаем:

ERR_С = 30х0,2 + 20х0,6 + 10х0,2 = 20%;

ERR_D= 115хО,2 + 80хО,6 + 45хО,2 = 80%.

По формуле (2):

О_С =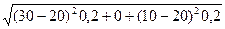= 6,3%;

О_С =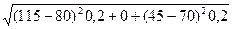= 22.14%;

Таким образом, у проекта D величина О намного больше, но при этом больше и значение ERR. Для того, чтобы можно было принять решение в пользу того или иного проекта, необходимо рассчитать коэффициент СУ, отражающий соотношение между ERR и О (рис. 6).

По формуле (5) получаем:

V_C = 6,3/20 = 0,315;

V_D = 22,14/80 = 0,276.

Как видно, несмотря на достаточно большое значение O, вели­чина V у проекта D меньше, т.е. меньше риска на единицу до­ходности, что достигается за счет достаточно большой величины ERR_D.

В данном случае расчет коэффициента СУ дает возможность принять решение в пользу второго проекта.

Однако необходимо отметить, что определение степени риска не всегда позволяет однозначно принять решение в пользу того или иного проекта.

Дата добавления: 2014-01-07