Универсальные факты

Переменные также полезны и в фактах. Предположим, что все библейские персонажи любят гранаты. Вместо того чтобы включать соответствующий факт для каждого индивида:

любит(авраам, гранаты).

любит(сара, гранаты).

все это можно выразить универсальным фактом любит(X, гранаты). В данном случае переменные позволяют выразить совокупность многих фактов. Факт умножить(0, X, 0) объединяет все факты, утверждающие, что 0, умноженный на любое число, дает 0.

Переменные в фактах неявно связаны квантором общности; это на интуитивном уровне означает, что факт любит(X, гранаты) утверждает, что для всех Х справедливо: X любит гранаты. В общем случае факт p (T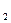,T,…,T). следует понимать так. что при любых значениях переменных X,...,X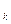, где X– переменные, входящие в факт p (T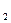,T,…,T). выполнено. Естественно, из факта с квантором общности можно вывести любой пример факта. Например, из любых(X, гранаты) следует любит(авраам, гранаты).

Это – третье правило вывода, называемое конкретизацией, из утверждения Р с квантором общности выводится пример Р Q при любой подстановке Q.

Как и в случае вопроса, можно добиться, чтобы два неопределенных объекта, обозначенных переменными, совпадали – для этого нужно использовать имя одной и той же переменной. Факт плюс(0, X, X) означает, что 0 является левой единицей по сложению. Это следует понимать так, что при всех значениях X, 0 плюс X равно X. Аналогичное использование переменных возникает при переводе фразы «каждый любит себя» в факт любит(X, X).

Поиск ответа на основной вопрос при использовании факта с квантором общности происходит непосредственно. Ищется факт, для которого вопрос является примером. Например, ответом на вопрос плюс(0, 2, 2) на основе факта плюс(0, X, X) будет да. Поиск ответа на неосновной вопрос при использовании неосновных фактов требует нового понятия: общий пример двух термов.

·Определение. С называется общим примером термов А и В. если С есть пример А и С есть пример B. Иными словами, если найдутся такие подстановки Qи Q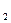, что С =AQсинтаксически совпадает с ВQ.·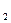

Например, цели плюс(0, 3, Y) и плюс(0, X, X) имеют общий пример плюс(0, 3, 3). Применения подстановки {Y = 3} к плюс(0, 3, Y) и подстановки {X = 3} к плюс(0, X, X) приводят к плюс(0, 3, 3).

В общем случае при поиске ответа на вопрос с использованием факта ищется общий пример вопроса и факта. Если общий пример существует, то он и будет, ответом. В противном случае ответ – нет.

Ответ на экзистенциальный вопрос на основе универсального факта с использованием общего примера требует двух логических выводов. Факт выводится из примера с помощью правила конкретизации, а пример выводится из вопроса с помощью правила обобщения.

Дата добавления: 2014-01-07