Запоминающие функции

Запоминающие функции сохраняют промежуточные результаты с цельюихиспользования в дальнейших вычислениях. Запоминание промежуточных результатов в чистом Прологе невозможно, поэтому реализация запоминающих функций основана на побочных эффектах. Такой способ программирования может быть назван программированием по восходящей методологии.

Исходной запоминающей функцией является функция lemma (Goal). Операционное понимание состоит в следующем: предпринимается попытка доказать цель Goal, и если попытка удалась, результат доказательства сохраняется в виде леммы. Отношение задается следующим образом;

lemma (Р) ¬Р, asserta((P ¬!)).

Следующая попытка доказать цель Р приведет к применению нового правила, что позволит избежать ненужного повторения вычислений. Отсечение введено для того, чтобы воспрепятствовать повторному рассмотрению всей программы. Применение отсечения обоснованно лишь в тех случаях, когда цель Р имеет не более одного решения.

Использование лемм демонстрируется на примере программы 12.3, описывающей решение задачи о ханойской башне. В ней радикально улучшены характеристики программы 3.30, решающей данную задачу. Хорошо известно, что решение задачи о ханойской башне с N дисками требует 2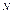- 1 перемещений. Например, в случае 10 дисков требуются 1023 перемещения или, в терминах программы 3.30, требуются 1023 обращения к процедуре hanoi(l.A,B,C,Xs). Суммарное число общих вызовов процедуры hanoi/5 будет существенно больше.

Решение задачи о ханойской башне состоит в повторяющемся решении подзадач о перемещении одного и того же количества дисков. Запоминающая функция может быть использована при повторном обращении к поиску перемещений, необходимых для решения задачи с меньшим числом дисков. В последующих попытках решить ту же подзадачу могут использоваться уже вычисленные последовательности перемещений вместо их перевычисления.

Эта идея реализована в рекурсивном предложении процедуры Hanoi в программе 12.3. В первом обращении к процедуре hanoi решается задача с N – 1 диском. Это решение запоминается и может быть использовано при втором обращении к процедуре hanoi с N – 1 диском.

Программа проверяется с помощью предиката test_hanoi(N, Pegs, Moves). Здесь N – число дисков. Pegs – список названий трех стержней, Moves – список перемещений, которые следует выполнить.Заметим что для эффективного использования запоминающих функций следует сначала решить общую задачу. Только после того, как общая задача полностью решена и запоминающие функции записали результат своей работы, можно задавать названия стержней.

hanoi(N,A,B,C,Moves)

Moves последовательность перемещений, необходимых для переноса N дисков со стержня А на стержень В с использованием промежуточного диска С. Перемещения производятся по правилам задачи о ханойской башне.

hanoi(l,A,B,C,[A to В]). hanoi(N,A,B,C,Moves) ¬

N > 1,

N1:= N - 1,

lemma(hanoi(N1,A,C,B,Ms1)),

hanoi (N1,C,B,A,Ms2),

append(Msl,[A to B | Ms2],Moves).

lemma(P) ¬P, asserta((P ¬!)),

Проверка

test_.hanoi(N, Pegs, Moves) ¬

hanoi(N, A, B,C, Moves), Pegs = [A,B,C].

Программа 12.3. решение задачи о ханойской башне с использованием запоминающих функций.

Дата добавления: 2014-01-07