Разностные структуры

Идея, лежащая в основе построения и применения разностных списков, состоит в использовании для представления частичных результатов вычислений разности неполных структур данных. Такой подход применим не только к спискам, но и к другим рекурсивным структурам данных. В этом разделе рассматривается один специфический пример, связанный с алгебраическими суммами.

Рассмотрим задачу нормализации арифметических выражений, например сумм. На рис. 15.3 представлены две суммы: (a+b)+(c+d) и (а+(b+(с+d))). Согласно стандартному синтаксису Пролога, скобки в терме а + b +с расставляются следующим образом: ((а+ b)+ с). Опишем процедуру преобразования суммы в нормализованную сумму, в которой сгруппированы правые скобки. Например, выражение, представленное на рис, 15.3 слева, должно быть преобразовано в нормализованное выражение, показанное справа. Такая процедура полезна для упрощения алгебраических выражений, облегчения написания программ проверки эквивалентности выражений.

Введем понятие разностной суммы как некоторого варианта разностного списка. Разностная сумма представлена структурой вида Е1 + + Е2, где Е1 и E2 – неполные нормализованные суммы. Предполагается,что + + является обозначением бинарного инфиксного оператора. Условимся также использовать 0 для обозначения пустой суммы.

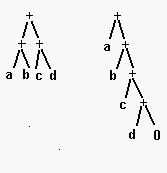
Рис 15.3. Ненормализованная и нормализованная суммы

Программа 15.7 является программой для нормализации сумм. Реляционной схемой программы является отношение normalize (Exp,NormExp}, где NormExp – выражение, эквивалентное выражению Ехр, в котором сгруппированы правые скобки при сохранении порядка констант, определенного в выражении Ехр.

normalize (Sum, NormalizedSiim) ¬

NormalizedSum – результат нормализации выражения Sum.

normalize(Exp,Norm) ¬ normalize._ds(Exp,Norm+ +0).

normalize_ds(A + В, Norm + + Space) ¬

normalize_ds(A, Norm+ +NormB),

normalize_ds(B, NormB + + Space).

normalize_ds(A,(A + Space) + +Space) ¬

constant (A).

Программа 15.7. Нормализация выражений типа «сумма».

По структуре эта программа подобна программе 15.2 для раскрытия списков с использованием разностных списков. Существует начальный этап установки разностной структуры, на котором обычно выполняется обращение к предикату с тем же именем, но имеющим другую арность или другой вид аргументов. Последнее предложение normaiize_ds в программе распространяет хвост неполной структуры данных, в то время как цели в теле рекурсивного предложения передают хвост первой неполной структуры во вторую структуру, где он занимает место головы структуры данных.

Программа строит нормализованную сумму по принципу сверху вниз. По аналогии с программами, использующими разностные списки, и эта программа может быть легко модифицирована, с тем, чтобы структура строилась снизу вверх (см. упражнение в конце раздела).

Эти программы имеют простой декларативный смысл. Операционное их толкование состоит в представлении процесса построения структуры путем ее наращивания, когда явно указывается «место» для последующих результатов. Здесь видна полная аналогия с разностными списками.

Дата добавления: 2014-01-07