Операции отрицания

Пусть множество значений функций принадлежности 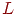является линейно упорядоченным множеством с наименьшим 0 и наибольшим 1 элементами. Примером 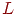может служить интервал вещественных чисел 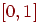, шкала лингвистических оценок (например, L={"неправдоподобно", "малоправдоподобно", "средняя правдоподобность", "большая правдоподобность", "наверняка"}, шкала балльных оценок и др.

Определение. Операцией отрицания на 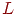называется функция , удовлетворяющая следующим условиям:

(О1) ;

(O2) .

В зависимости от выполнения на 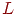дополнительных условий, рассматриваются следующие типы отрицаний:

· Строгое отрицание: ;

· Квазистрогое отрицание: ;

· Инволюция: ;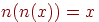

· Обычное отрицание: ;

· Слабое отрицание: .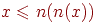

Слабое отрицание называется также интуиционистским отрицанием. Элемент 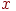из 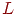будет называться иволютивным элементом, если 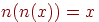, в противном случае он будет называться неиволютивным. Отрицание будет называться неиволютивным, если 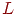содержит неиволютивные по этому отрицанию элементы.

Элемент , удовлетворяющий условию , называется фиксированной точкой. Этот элемент будет центральным элементом (фокусом) 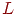. Очевидно, что если фиксированная точка существует, то она единственна.

Отрицание называется сжимающим в точке , если выполнено условие

Отрицание называется сжимающим на 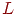, если оно сжимающее в каждой точке множества .

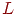Отрицание называется разжимающим в точке , если выполнено условие

Отрицание называется разжимающим на 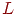, если оно является разжимающим в каждой точке множества .

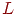Теорема Для любого отрицания любая точка является либо сжимающей, либо разжимающей.

Доказательство Пусть 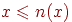, тогда из условия (О2) получим 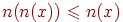, откуда следует либо , либо . Аналогично, из получаем , и, следовательно, либо , либо

Следствие Элемент 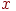является иволютивным тогда и только тогда, если он одновременно сжимающий и разжимающий.

Используя математические методы, можно доказать, что элементы, порождаемые сжимающими и разжимающими отрицаниями в точках, представляют собой спирали, соответственно "закручиваемые внутрь" или "раскручиваемые наружу". Эти спирали либо бесконечные, либо в конечном случае имеют петлю на конце, состоящую из двух элементов, которые для сжимающих отрицаний могут совпадать, образуя неподвижную точку отрицания. Спирали, порождаемые разными элементами, либо вложены друг в друга, либо совпадают, начиная с некоторого элемента.

На рис. 8.1 даны примеры сжимающего и разжимающего в точке 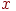отрицания. Элементы 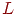представлены вершинами соответствующего графа и упорядочены снизу вверх, в частности, . Элементы y порождаются элементами 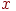так, что 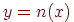для рис. 8.1(А) и для рис. 8.1(Б).

Рис. 8.1.

Рассмотрим простейшие примеры отрицаний. Во всех примерах предполагается, что 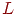содержит элементы, отличные от 0 и 1.

Пример. "Все, что не истина и не ложь, является неопределенностью".

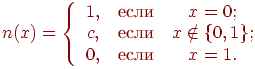
Рис. 8.2.

где 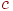– некоторый элемент из 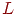такой, что . Это отрицание является сжимающим, ни обычным, ни слабым, с фиксированной точкой.

Пример. "Все, что не истина, есть ложь".

Рис. 8.3.

Это отрицание является обычным, разжимающим, квазистрогим, без фиксированной точки.

Пример. "Все, что не ложь, есть истина".

Рис. 8.4.

Это отрицание является слабым, разжимающим, квазистрогим, без фиксированной точки.

Пример. "Все или истина, или ложь".

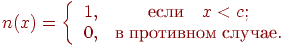
Рис. 8.5.

где 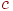– некоторый элемент из 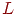такой, что .

Это отрицание является разжимающим, ни обычным, ни слабым, без фиксированной точки. Некоторые подходы к формализации нечеткой логики, основанные на подобной интерпретации, сводят ее к двузначной, используя .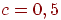

Пример. Пусть , где .

Рис. 8.6.

Это отрицание является иволютивным. При нечетном фиксированной точкой отрицания является элемент 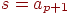. Мера нечеткости на этом элементе принимает максимальное значение. При четном фиксированная точка отрицания отсутствует, фокус состоит из множества 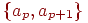, имеющих максимальную нечеткость.

Пример. "Все, что не истина, есть ложь".

Рис. 8.3.

Это отрицание является обычным, разжимающим, квазистрогим, без фиксированной точки.

Пример. "Все, что не ложь, есть истина".

Рис. 8.4.

Это отрицание является слабым, разжимающим, квазистрогим, без фиксированной точки.

Пример. "Все или истина, или ложь".

Рис. 8.5.

где 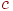– некоторый элемент из 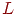такой, что .

Это отрицание является разжимающим, ни обычным, ни слабым, без фиксированной точки. Некоторые подходы к формализации нечеткой логики, основанные на подобной интерпретации, сводят ее к двузначной, используя .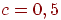

Пример. Пусть , где .

Рис. 8.6.

Это отрицание является иволютивным. При нечетном фиксированной точкой отрицания является элемент 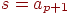. Мера нечеткости на этом элементе принимает максимальное значение. При четном фиксированная точка отрицания отсутствует, фокус состоит из множества 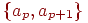, имеющих максимальную нечеткость.

Дата добавления: 2014-01-07