Теории металлов

1. Высокая электропроводность металлов обусловлена высокой концентрацией в них носителей тока – электронов проводимости. Электроны проводимости рассматриваются как электронный газ, обладающий свойствами идеального одноатомного газа. Концентрация электронов проводимости в металлах порядка 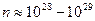м3. В отсутствие электрического поля электроны проводимости движутся 1. Высокая электропроводность металлов обусловлена высокой концентрацией в них носителей хаотически, поэтому электрического тока не возникает. Средняя кинетическая энергия теплового движения электронов проводимости определяется по уравнению:

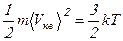, (10.8)

где - масса электрона проводимости;- средняя квадратичная скорость электрона проводимости.

При температуре 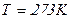средняя квадратичная скорость теплового движения электронов проводимости .

2. Электрический ток в металле возникает под действием электрического поля, которое вызывает направленное, т.е. упорядоченное, движения носителей тока. Направлено это движение всегда против поля, т.к. заряд электрона отрицательный, а за направление тока и вектора плотности тока принято направление движения положительных зарядов. Запишем уравнение для плотности тока проводимости – через поперечное сечение проводника площадью S за время t пройдут все электроны, находящиеся в проводнике высотой (Рис.5).

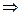
, (10.9) где - концентрация носителей тока; 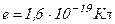- заряд электрона; - средняя скорость направленного движения электронов проводимости.

Оценим величину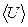при самых больших допускаемых в эксплуатации значениях плотности тока, например,.Расчет, показывает что .

Таким образом, средняя скорость направленного движения электронов много меньше, чем скорость их теплового движения 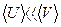. Но именно скорость направленного движения обеспечивает наличие тока в проводнике. При включении электрического тока поле в проводнике смещает все хаотически движущиеся электроны в одном направлении.

3. При своем движении электроны сталкиваются с узлами кристаллической решетки (ионами), которые совершают беспорядочные тепловые колебания около положений равновесия. Считается, что средняя длина свободного пробега электронов (расстояние, проходимое между двумя столкновениями) равна расстоянию между узлами кристаллической решетки (параметру решетки), т.е. .

4. В классической теории принято, что соударение электронов проводимости с узлами решетки происходит по типу неупругого удара. Электроны в таком случае теряют всю энергию, которую они приобрели при направленном движении под действием электрического поля:

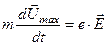
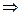
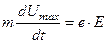. (10.10)

Скорость упорядоченного движения электронов, следовательно, изменяется от своего максимального значения перед столкновением, т.е. после прохождения расстояния между узлами решетки до нуля в момент столкновения, Проинтегрировав уравнение (10.10) по времени от 0 до , где - средняя продолжительность пробега. Определим максимальную скорость направленного движения электрона в электрическом поле:

.

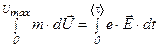
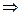
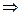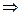
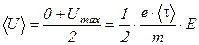(10.11) Электрон проводимости одновременно участвует в тепловом и направленном движении. Учитывая, что 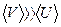, определим среднюю продолжительность пробега:

(10.12) Подставив найденное значение средней продолжительности пробега электрона в уравнение (11) и учитывая, что 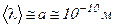, получаем:

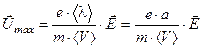
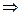
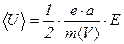. (10.13)

Таким образом, классическая электронная теория основана на предположении, что:

- поведение свободных электронов в металле (носителей тока) определяется законами Ньютона;

- газ свободных электронов в металле - идеальный газ;

- электроны, двигаясь в кристаллической решетке, испытывают неупругое соударение с каждым узлом кристаллической решетки, встречающимся на его пути; следовательно, его путь от столкновения до столкновения , равный параметру кристаллической решетки металла (), является величиной постоянной.

Подставив уравнение (10.13) в уравнение (10.9) поучим выражение закона Ома в дифференциальной форме:

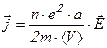
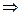
, (10.14) где 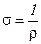- удельная электропроводность, величина обратно пропорциональная удельному сопротивлению проводника. Из уравнения (10.14) следует, что . (10.15)

Проанализируем, от каких величин зависит удельная электропроводность. В выражение (10.15) входит лишь одна величина, которая меняется, это скорость теплового движения электрона проводимости - 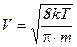. Все остальные величины постоянны. Следовательно, 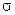~ и 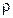~ 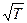. По экспериментальным данным сопротивление проводника с температурой изменяется по линейному закону, т.е. 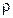~ (Рис.6).

- по шкале Цельсия 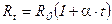или - по шкале Кельвина .

Классическая электронная теория металлов не может объяснить этого затруднения. Объяснение было дано лишь в рамках квантовой теории.

Дата добавления: 2014-01-07