Где - концентрация, т.е. число молекул в единице объема

Молекулы в газе, находясь в состоянии непрерывного хаотического движения, сталкиваются друг с другом. Между столкновениями они проходят свободно некоторый путь. Длина пути между двумя столкновениями различна, но благодаря большому числу молекул и беспорядочности их движения можно говорить о средней длине свободного пути молекулы. Определим среднюю длину свободного пути молекул -.

Молекул в газе

Число столкновений и длина свободного пробега

Для вывода основных закономерностей явлений переноса с помощью молекулярно-кинетической теории необходимо предварительно определить длину свободного пробега молекул в газах и выяснить её зависимость от состояния газа.

Рассмотрим молекулу, которая движется со скоростью 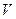. Представим её в виде шарика радиуса . После каждого столкновения молекула меняет направление скорости, однако, для простоты рассуждений предположим, что молекула после столкновения продолжает двигаться в том же направлении, в каком она двигалась до столкновения. Кроме того, предположим, что все другие молекулы, кроме рассматриваемой молекулы, неподвижны. Тогда молекула при своем движении заденет все те молекулы, центры которых лежат на расстоянии не больше от прямой вдоль которой она движется (Рис.1).

Следовательно, за единицу времени молекула заденет все те молекул, центры которых лежат внутри цилиндра радиуса и длины , численно равной скорости молекулы 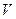(Рис.2).

Величина называется эффективным диаметром молекулы; - эффективное сечение молекулы. Молекулы – это сложные системы, состоящие из атомных ядер и электронов. Силы взаимодействия между ними, которые действуют на малых расстояниях, носят сложный характер. Процесс столкновения сводится к тому, что на малых расстояниях молекулы отталкиваются друг от друга, причем силы отталкивания возрастают по мере уменьшения расстояния между ними. Поэтому эффективный диаметром молекулы, введенный в предположении, что молекулы упругие шарики, дает лишь приближенное представление о размерах молекул. Установлено, что величина зависит от температуры:

, или (7.4)

где - радиус молекулы без учета сил взаимодействия; - постоянная Сезерленда.

Число молекул 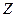, центры которых попадают внутрь цилиндра радиуса , равно:

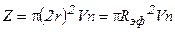, (7.5)

Для среднего числа столкновений в единицу времени получим выражение:

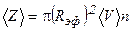(7.6)

Так как на самом деле движутся все молекулы, то для числа столкновений получается несколько большее значение:

. (7.7)

Среднюю длину свободного пробега молекулы получим, поделив средний путь, проходимый ею за единицу времени, на число столкновений в единицу времени 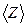. Так как путь, проходимый в единицу времени, численно равен скорости , то средняя длина свободного пробега может быть определена по уравнению:

, (7.8)

Если вспомнить, что 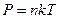, то уравнение (7.7) принимает вид:

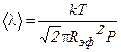. (7.9)

Оценим на численном примере число столкновений, испытываемых молекулой кислорода при нормальных условиях - и 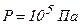, приняв эффективный диаметр молекулы равным . Для этого рассчитаем:

концентрацию молекул ;

среднюю скорость молекул ;

среднюю длину свободного пробега ;

Дата добавления: 2014-01-07