
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проводники в электрическом поле
|
|
|
|
Проводник представляет собой тело, содержащее свободные электроны, заряды которых скомпенсированы положительными зарядами узлов кристаллической решетки. Мы рассматриваем электростатику, поэтому заряды внутри проводника неподвижны, т.е. находятся в равновесии. Необходимым условием равновесия зарядов внутри проводника является равенство нулю напряженности электростатического поля. Если бы напряженность поля не была бы равна нулю, то возникали бы электрические силы, пропорциональные напряженности, под действием этих сил заряды двигались бы. С другой стороны, учитывая связь между напряженностью потенциалом, имеем:


 (9.1)
(9.1)
Условие(9.1) приводит к тому, что в заряженном проводнике некомпенсированные заряды могут располагаться лишь на поверхности проводника. Причем вектор напряженности должен быть направлен по нормали к поверхности проводника -  . Иначе под действием составляющей вектора напряженности, касательной к поверхности проводника
. Иначе под действием составляющей вектора напряженности, касательной к поверхности проводника  , заряды перемещались бы по поверхности проводника, что противоречит их статическому распределению ( Рис.1).
, заряды перемещались бы по поверхности проводника, что противоречит их статическому распределению ( Рис.1).

Отсюда следует:
- во всех точках внутри проводника напряженность поля равна нулю;
- составляющая вектора напряженности, касательная к поверхности проводника  ;
;
- весь объем проводника является эквипотенциальным объемом потому, что 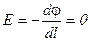 и, следовательно,
и, следовательно, 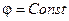 . Эквипотенциальна и поверхность проводника, т.к.
. Эквипотенциальна и поверхность проводника, т.к. 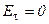 ;
;
- в заряженном проводнике некомпенсированные заряды располагаются только на внешней поверхности проводника, т.к. во всех точках внутри проводника отсутствует электрическое поле  ,.
,.
При внесении незаряженного проводника в электрическое поле носители свободных зарядов приходят в движение: положительные в направлении вектора 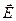 , отрицательные – в противоположном направлении. В результате на концах проводника возникают заряды противоположного знака, которые называются индуцированными. Эти заряды создают поле, напряженность которого противоположна по направлению внешнему (Рис.2).
, отрицательные – в противоположном направлении. В результате на концах проводника возникают заряды противоположного знака, которые называются индуцированными. Эти заряды создают поле, напряженность которого противоположна по направлению внешнему (Рис.2).
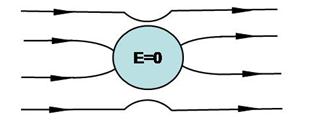
Перераспределение зарядов будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника – перпендикулярными к его поверхности. Таким образом, нейтральный проводник, внесенный в электрическое поле, разрывает часть линий напряженности. Они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. На явлении распределения зарядов по внешней поверхности основана электростатическая защита.
Определим напряженность поля вблизи поверхности проводника, которому сообщен избыточный заряд. Воспользуемся теоремой Гаусса. Выделим на поверхности проводника малую площадку и построим на ней произвольную замкнутую поверхность – цилиндр, ось которого перпендикулярна поверхности (Рис.3).
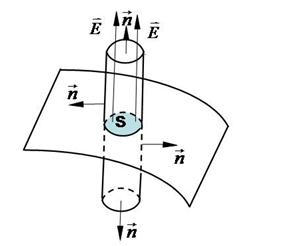
Верхнее основание цилиндра расположено вне проводника, а нижнее – внутри. Поток вектора напряженности через произвольную замкнутую поверхность будет равен потоку через верхнее основание цилиндра  , т.к. заряды находятся лишь на внешней поверхности проводника. Заряд внутри произвольной поверхности (в нашем случае цилиндра) равен
, т.к. заряды находятся лишь на внешней поверхности проводника. Заряд внутри произвольной поверхности (в нашем случае цилиндра) равен 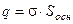 . Теперь запишем уравнение теоремы Гаусса и определим напряженность поля вблизи поверхности заряженного проводника:
. Теперь запишем уравнение теоремы Гаусса и определим напряженность поля вблизи поверхности заряженного проводника:
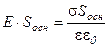

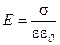 . (9.2)
. (9.2)
Напряженность электрического поля зависит от свойств среды ( ). Для характеристики поля целесообразно ввести величину, которая бы не зависела от свойств. Этому условию удовлетворяет физическая величина, которая называется электрическим смещением или электрической индукцией:
). Для характеристики поля целесообразно ввести величину, которая бы не зависела от свойств. Этому условию удовлетворяет физическая величина, которая называется электрическим смещением или электрической индукцией:
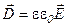 . (9.3)
. (9.3)
По уравнению (9.2) следует, что 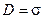 .
.
Таким образом, если электростатическое поле создано заряженным проводником, то напряженность этого поля вблизи поверхности проводника прямо пропорциональна поверхностной плотности зарядов, находящихся на проводнике. Причем вектор напряженности должен быть направлен по нормали к поверхности проводника - 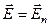 .
.
 Распределение зарядов по внешней поверхности проводника зависит от её формы. Чтобы убедиться в этом, воспользуемся законом сохранения заряда. Рассмотрим два проводника в виде шаров с радиусами R1 > R2. Если их соединить между собой проводником (Рис.4), то потенциалы проводников выровняются -
Распределение зарядов по внешней поверхности проводника зависит от её формы. Чтобы убедиться в этом, воспользуемся законом сохранения заряда. Рассмотрим два проводника в виде шаров с радиусами R1 > R2. Если их соединить между собой проводником (Рис.4), то потенциалы проводников выровняются - 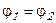 , а заряды перераспределяться между проводниками.
, а заряды перераспределяться между проводниками.
Отсюда получаем:
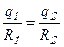





 ~
~  . (9.4)
. (9.4)
 Итак, где кривизна поверхности больше, там и поверхностная плотность заряда выше. На внутренних поверхностях замкнутых полых проводников избыточные заряды отсутствуют и
Итак, где кривизна поверхности больше, там и поверхностная плотность заряда выше. На внутренних поверхностях замкнутых полых проводников избыточные заряды отсутствуют и 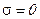 . Распределение заряда по поверхности проводника можно оценить экспериментально, используя проводник сложной формы (Рис.5).
. Распределение заряда по поверхности проводника можно оценить экспериментально, используя проводник сложной формы (Рис.5).
Опыт показывает, что самая большая плотность зарядов будет на острие проводника (точка 1). Внутри проводника заряды отсутствуют (точки 2). Во всех точках цилиндрической части поверхности проводника (точки 3), где кривизна одинакова, поверхностная плотность зарядов одинакова.
Большая поверхностная плотность заряда на острие проводника приводит к большой напряженности поля вблизи острия. В атмосферном воздухе всегда присутствует небольшое число положительных ионов и свободных электронов. В сильном электрическом поле около острия, положительно заряженные ионы движутся с большой скоростью и, сталкиваясь с молекулами воздуха, ионизируют их. Возникает явление «электрического ветра». Вследствие сильной ионизации воздуха вблизи острия оно быстро теряет электрический заряд. Поэтому для сохранения заряда на проводниках стремятся к тому, чтобы проводники не имели острых выступов.
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1025; Нарушение авторских прав?; Мы поможем в написании вашей работы!