Энергия электрического поля

Энергия заряженного проводника.

Подсчитаем энергию уединенного заряженного проводника. Для зарядки проводника необходимо совершить работу. Она является мерой энергии заряженного проводника, которая аналогична потенциальной энергии в механике. Эта работа может быть получена обратно при разрядке проводника. Подсчитаем работу зарядки. Предполагаем, что проводник, у которого электроемкость С, первоначально незаряженный, получает заряд q и при этом его потенциал принимает значение φ. Работа, совершаемая против сил электростатического поля при перенесении заряда dq из бесконечности на проводник равна:

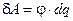, учитывая соотношение 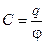, получаем 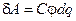. (9.13)

Для того чтобы зарядить тело от нулевого потенциала до потенциала φ, необходимо совершить работу:

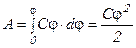. (9.14)

Очевидно, что энергия заряженного тела равна той работе, которую необходимо совершить, чтобы зарядить это тело. Таким образом, уравнение (9.14) определяет энергию заряженного тела:

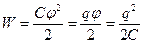. (9.15)

Полученные уравнения для энергии легко обобщить и на случай заряженного конденсатора. Процесс зарядки пластин можно представить следующим образом. Первоначально нейтральные пластины постепенно заряжаются переносом бесконечно малого заряда 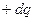с одной пластины на другую. Этот перенос увеличивает положительный заряд одной пластины и уменьшает положительный заряд, или, что-то же самое, увеличивает отрицательный заряд другой пластины на такую же величину. Таким образом, в процессе зарядки, на обеих пластинах имеем заряды равные по величине и противоположные по знаку. Перенос заряда с одной пластины на другую требует совершения работы:

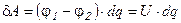
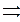
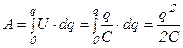. (9.16)

Эта работа определяет энергию заряженного конденсатора:

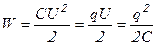(9.17)

Выразим энергию заряженного конденсатора через величины, которые характеризуют поле между обкладками конденсатора. Для этого вспомним, как можно выразить емкость конденсатора, разность потенциалов между обкладками, а так же связь между напряженностью электрическим смещением поля:

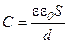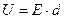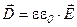; ; (9.18)

Уравнение (9.17) после подстановки уравнений (9.18) принимает вид:

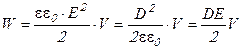. (9.19)

Для сравнения различных полей введем величину объемная плотность энергии:

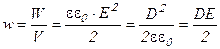(9.20)

Таким образом, энергия электрического поля заключена в объеме между его обкладками 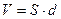и определяется его характеристиками – напряженностью (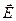) или электростатической индукцией ().

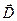Дата добавления: 2014-01-07