Закон Ампера. Взаимодействие параллельных токов

Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила 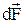,с которой магнитное поле действует на элемент проводника 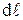с током, находящийся в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной 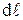проводника на магнитную индукцию :

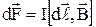. (3.8)

Направление вектора 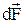может быть найдено, согласно (3.8), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор , а четыре вы­тянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы Ампера (см. 3.8) вычисляется по формуле

dF=IBd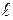sin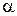, (3.9)

где α - угол между векторам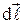и и .

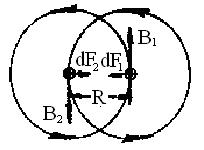Рис. 37

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2 (направления токов указаны на рис. 37), расстояние между которыми равно R. Каждый из проводников создает магнит­ное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент 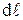второго проводника с током I2.

Каждый из проводников создает магнит­ное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I₁ на элемент 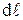второго проводника с током I₂.

Ток I₁ создает вокруг себя магнитное поле, линии магнитной индукции ко­торого представляют собой концентрические окружности. Направление вектора В задается правилом правого винта, его модуль по формуле (3.7) равен

.

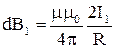Направление силы 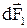, с которой поле 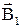действует на участок 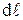второ­го тока, определяется по правилу левой руки и указано на рис 37. Модуль силы, согласно (3.9), с учетом того, что угол а между элементами тока І₂ и вектором 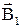прямой равен

,

или, подставляя значения для В₁ получим

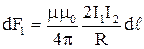. (3.10)

Рассуждая аналогично, можно показать, что сила dF₂, с которой магнитное поле тока І₂ действует на элемент d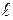первого проводника с током І₁ направле­на в противоположную сторону и по модулю равна

. (3.11)

Сравнение выражений (3.10) и (3.11) показывает, что

dF₁ = dF₂,

т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой

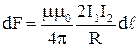. (3.12)

Еслии токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, оп­ределяемая формулой (3.12).

Дата добавления: 2014-01-07