Имитационный и оптимизационный режимы построения математических моделей объектов и явлений

Заметим, что характер систематизации определяется качественными частными критериями, поддающимися только типизации. В этом случае разрабатывается шкала дискретных оценок показателей или качественных критериев из девяти уровней оценки. Такая шкала может быть положена в основу анкеты для морфологического анализа состояния природных ресурсов при их хозяйственном использовании.

Модели, возникающие в процессе системного анализа, могут быть использованы в оптимизационном или имитационном режимах. При отсутствии точной формулировки цели исследования или поведения система изучается в имитационном режиме по определенному сценарию, в котором определяется последовательность изменения свободных функций или параметров. По результатам такого процесса вырабатываются или уточняются критерии, которые затем используются для анализа модели в оптимизационном режиме.

Оптимизационный режим реализуется при заданной целевой функции, когда может быть сделан выбор свободных параметров, обеспечивающий ее экстремальное значение.

Среди системных моделей, наиболее соответствующих информационно-технологическому подходу выделяются балансовые имитационные динамические модели Дж. Форрестера.

Балансовые модели Форрестера направлены на комплексное решение хозяйственной деятельности предприятий в инфраструктуре розничной и оптовой торговли и оценку динамики развития городов и мирового хозяйства. Однако, при создании системных методов анализа сложных комплексов могут быть учтены особенности взаимодействия различных видов хозяйственной деятельности с природными ресурсами. При таком подходе целью планирования является национально-экономическое развитие и качество окружающей среды.

4. Приложения методов системного анализа к вопросам природопользования и оценка устойчивости их решений.

Известны системные комплексы типа «Человек – вода - лес», которые демонстрируют возможности концепции балансово-информационного моделирования систем с обратной связью как основополагающего принципа описания любой планируемой системы. Несмотря на то, что система «Человек – вода - лес» имеет 110 идентификаторов, описывающих элементы системы (темпы, уровни состояния потоков субстанций и множители связи подсистем) она является ограниченной. Ее недостатком следует считать, с одной стороны, косвенный учет природных факторов, которые учитываются в виде загрязнений, а с другой – исключение из рассмотрения почвенно-климатических, атмосферных и иных природных компонентов.

Устойчивость природных компонентов модели определяется способностью траекторий ее основных функций приближаться к точкам равновесия или неподвижным точкам фазового пространства, что с математической точки зрения определяет термин «аттрактор». Фазовое пространство имеет смысл математического пространства, в котором переменными являются обобщенные координаты и обобщенные импульсы. В динамических системах, задаваемых системой эволюционных уравнений первого порядка, координатами служат переменные состояния, или компоненты вектора состояния.

Примером модели, учитывающей пространственную неоднородность природных факторов, является Стенфордская модель формирования стока с речного водосбора. Модель, разработанная под руководством Р.К.Линсея, основана на принципе водного баланса с учетом поверхностного и подповерхностного стока, инфильтрации через капиллярную систему почвы, фильтрации и поверхностного задержания. Разработаны варианты модели, преследующие попытку описать комплекс всех процессов, происходящих на водосборе.

В последнем варианте Стендфордской модели число контролируемых параметров достигает 30. Модель позволяет проводить численные эксперименты в имитационном режиме по выявлению влияния антропогенных воздействий на изменение различных физико-географических факторов, водный баланс и режим стока. Приведем схему модели в обозначениях Форрестера (рис.1).

Анализ Стенфордской модели в обозначениях Форрестера показывает, что она охватывает только материальные потоки субстанций. Элементы структуры модели имеют информационные связи, которые характеризуют ее регулирующие функции. Например, темпы (13, 14, 15), могут быть охвачены информационными связями: русловое регулирование (13), является результатом действия водозаборов (14) и регулирования стока водохранилища (15).

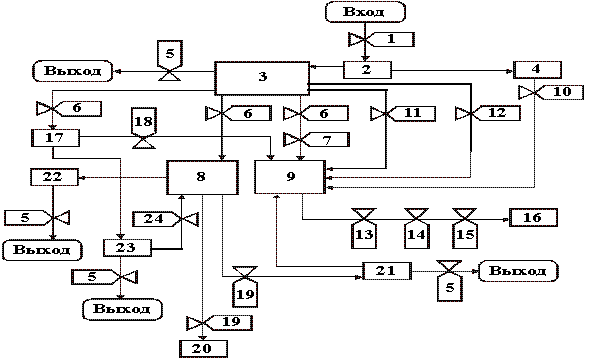
Рис. 2.9. Блок-схема Стенфордской модели в обозначениях Форрестера:

1 - темп изменения выпадения осадков; 2 – уровень выпадения осадков;

3 – влагозапасы; 4 – снегозапасы; 5 – испарение; 6 – инфильтрация;

7 – подповерхностный сток; 8 – нижний слой и грунтовые воды;

9 – приток в русло; 10 – снеготаяние; 11 – подповерхностный сток;

12 – водонепроницаемая территория; 13 – русловое регулирование;

14 – водозаборы; 15 – регулирование стока водохранилищем;

16 – речной сток; 17 – верхний слой почвы; 18 – поверхностный сток;

19 – просачивание; 20 – пассивные запасы; 21 – запасы грунтовых вод; 22, 23 – влагозапасы;

24 – истощение влагозапаса верхнего слоя

Темпы (элементы 1, 5, 6, 7, 10, 11, 12, 13, 14, 15, 18, 19, 24) и уровни (элементы 2, 3, 4, 8, 9, 16, 17, 20, 21, 22, 23) в форрестеровской модели связываются информационными связями через функции или множители влияния. Введение таких функций или, в первом приближении, множителей позволяет снизить степень неопределенности модели и приблизить ее к оптимизационной. Гибкость модели при этом понижается, но возрастает степень ее определенности и однозначности.

Обычно модели природоресурсного характера подразделяются на детерминированные и стохастические. Последние используют понятия математической статистики. В частности, простейшие модели формирования стока с площади водосбора основаны на интеграле Дюамеля и используются для прогнозов гидрографов дождевых паводков и весеннего половодья.

Например, лесные биогеоценозы являются наиболее характерным примером сложных систем природного характера. Для сохранения экологического и ресурсного потенциала лесов и устойчивого экономического развития использования лесных ресурсов разработана «Концепция устойчивого управления лесами Российской Федерации» и «Критерии и индикаторы устойчивого управления лесами Российской Федерации».

В работах отечественных лесоводов появилось явное стремление дать точное определение понятия экологической устойчивости и определить связь этого понятия с понятием математической устойчивости. Первоначальные попытки описания сложных экосистем сводились к эвристическим методам оценки на основе биотехнического закона, основанного на интегральном представлении логистического уравнения или уравнения роста популяции:

х _n+1 = a x _n – b x _n².

Первый член уравнения в правой части описывает рост, а нелинейный член ответственен за ограничение роста, связанное, например, с ограниченностью энергетических или пищевых ресурсов. Пренебрегая в этом уравнении, записанном в конечных разностях, нелинейным членом (b = 0), можно выписать явное решение получающегося линейного уравнения:

x _n+1 = a x _n; x _n = x₀ a ⁿ.

Это решение устойчиво при ç а ç< 1 и неустойчиво при ç а ç> 1.

Н.Ф.Раймерсом создана классификация устойчивости экосистем, включающая устойчивость эволюционную, историческую и действующую.

Анализ экосистем показывает, что многие проблемы хозяйственного природопользования, если не подавляющее их большинство, определяется не дефицитом ресурсов, а состоит в незнании законов, управляющих параметрами природопользовательских комплексов.

5. Устойчивость решений, полученных на основе балансовых моделей.

При изучении динамики популяции обычно выделяется две группы моделей. К первой группе относятся математические модели, созданные на основе работ Николсона и Бейли для взаимодействия между хозяином и паразитом с дискретным размножением. Ко второй группе относятся континуальные модели на основе дифференциальных уравнений первого порядка, ведущие происхождение от модели Лотки - Вольтерры для оценки динамики популяций хищника и жертвы.

Однако, с математической точки зрения, выделенные группы являются вариантами записи одного и того же математического объекта. При этом первая группа моделей описывается в форме отображения Пуанкаре для динамической системы.

Отображение представляет собой выборку данных [х(t₁), х(t₂), …, х(t_n),…, х(t_N)], для которой вводится обозначение х_n = х(t_n). Величину х_n+1 можно найти в результате итеративного процесса по х_n. В конечном итоге получается разностное уравнение

х_n+1= f(х_n).

Если х_n = х(t_n) и y_n = dх(t_n)/dt, то в фазовой плоскости [х(t), dх(t)/dt] возникает двумерное отображение Пуанкаре

х_n+1= f(х_n, y_n);

y_n+1= g(х_n, y_n),

если t_n = nT + t₀, где Т – период временных выборок; t₀ – начальный период времени (рис.).

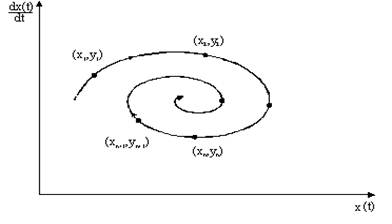
Рис. Временная эволюция на фазовой плоскости

Дата добавления: 2014-01-07