Вероятностно-статистические методы. Вероятность случайной величины

Вероятностью р(х) события х называют отношение числа случаев N(x), которые приводят к наступлению события х к общему числу возможных случаев N:

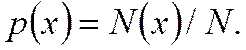
В математической статистике важное значение имеет понятие о частоте события 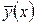, представляющей собой отношение числа случаев п(х), при которых имело место событие к общему числу событий п:

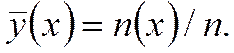
При неограниченном возрастании числа событий частота 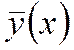стремится к вероятности 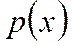. Частота 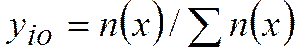характеризует вероятность появлений случайной величины и представляет собой ряд распределения (рис.7.6), а плавная кривая - закон (функцию) распределения F(x).

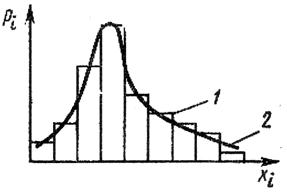
Рис. Общий вид распределения случайных величин:

1 – гистограмма; 2 – кривая распределения

Вероятность случайной величины (события) - это количественная оценка возможности ее появления, Достоверное событие имеет вероятность 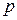=1, невозможное событие . Следовательно, для случайного события 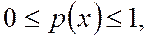, а сумма вероятностей всех возможных значений

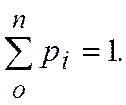
В исследованиях иногда недостаточно знать функцию распределения Необходимо также иметь ее характеристики:

1) среднеарифметическое значение,

2) математическое ожидание

3) дисперсию,

4) размах ряда распределения.

Пусть среди 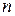событий случайная величина повторяется 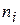раз, величина 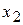- 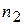раза и т.д. Тогда среднеарифметическое значение х имеет вид

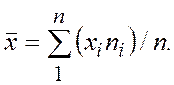
Размах можно использовать для ориентировочной оценки вариации ряда событий:

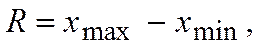
где 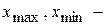максимальное и минимальное значения измеренной величины или погрешности.

Если вместо эмпирических частот 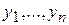принять их вероятности 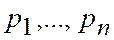, то это даст важную характеристику распределения - математическое ожидание:

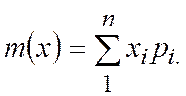
Для непрерывных случайных величин математическое ожидание определяется интегралом

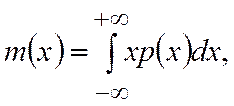
т.е. оно равно действительному значению 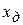наблюдаемых событии. Таким образом, если систематические погрешности измерений полностью исключены, то истинное значение измеряемой величины равно математическому ожиданию, а соответствующая ему абсцисса называется центром распределения. Площадь, расположенная под кривой распределения (рис.7.6), соответствует единице вследствие того, что кривая охватывает все результаты измерений. Для одной и той же площади можно построить большое количество кривых распределения, т.е. они могут иметь различное рассеяние. Мерой рассеяния (точности измерений) является дисперсия или среднеквадратичное отклонение. Таким образом, дисперсия характеризует рассеивание случайной величины по отношению к математическому ожиданию и вычисляется с помощью формулы

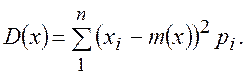
Важной характеристикой теоретической кривой распределения является среднеквадратичное отклонение:

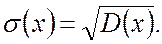
Коэффициент вариации

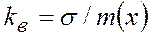
применяется для сравнения интенсивности рассеяния в различных совокупностях, определяется в относительных единицах (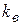<1).

10. Виды распределения случайных величин. Нормальное распределение, распределение Пуассона, закон распределения Вейбулла.

Основной задачей статистики является подбор теоретических кривых по имеющемуся эмпирическому закону распределения. Пусть в результате 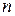измерений случайной величины получен ряд ее значений 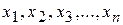. При первичной обработке таких рядов их вначале группируют в интервалы и устанавливают для каждого из них частоты 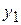и 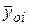. По значениям и 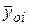строят ступенчатую гистограмму частот и вычисляют характеристики эмпирической кривой распределения. Основными характеристиками эмпирического распределения являются среднеарифметическое значение 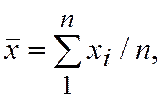дисперсия
и среднеквадратичное отклонение 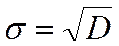. Значения этих величин соответствуют величинам 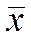, D(x) и 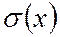теоретического распределения.

В исследованиях наиболее часто применяется закон нормального распределения (рис.1)

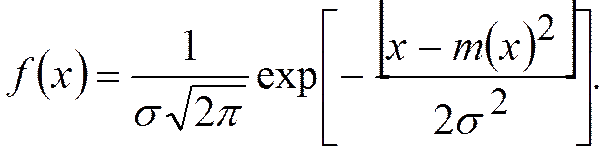
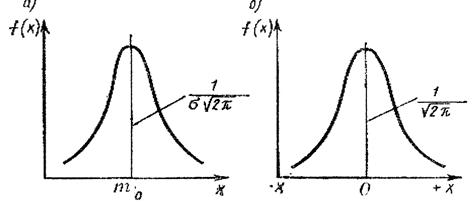
Рис.1. Общий вид кривой нормального распределения:

а - 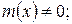б -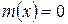

Это уравнение соответствует функции нормального распределения при (рис.6.7, а). Если совместить ось ординат с точкой 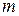, т.е. 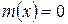(рис.6.7, б), и принять 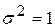, то закон нормального распределения описывается зависимостью

если за единицу масштаба принять дисперсию .

Для оценки рассеяния обычно пользуются величиной 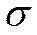. Чем меньше 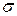, тем меньше рассеяние, т.е. большинство наблюдений мало отличается друг от друга (рис.2).

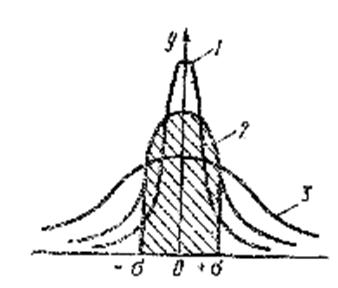
Рис.2. Характер рассеяния кривой нормального распределения:

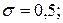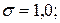1 - 2 - 3 -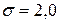

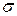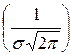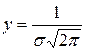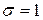С увеличением рассеяние возрастает, вероятность появления больших погрешностей увеличивается, а максимум кривой распределения (ордината, равная ) уменьшается. Поэтому величину при или 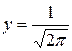называют мерой точности.

Таким образом, чем меньше 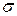, тем больше сходимость результатов измерений, а ряд измерений более точен, среднеквадратичное отклонение определяет закон распределения. Отклонения 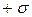и 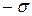соответствуют точкам перегиба кривой (заштрихованная площадь на рис.2), Вероятность того, что случайные события не выйдут за эти пределы, составляет 0,683. В общем случае для предела 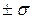вероятность того, что событие попадает о данный предел, вычисляется по распределению Лапласа

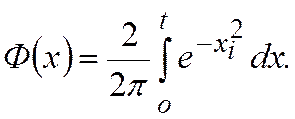
При анализе многих случайных дискретных процессов пользуются распределением Пуассона.

Так, вероятность появления числа событий х = 1,2,3,... в единицу времени определяется законом Пуассона (рис.3) и подсчитывается по формуле

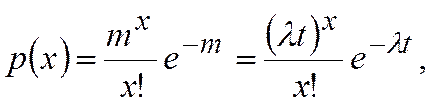
где х - число событий за данный отрезок времени 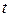; - плотность, т.е. среднее число событий за единицу времени; 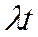- число событий за время t, .

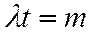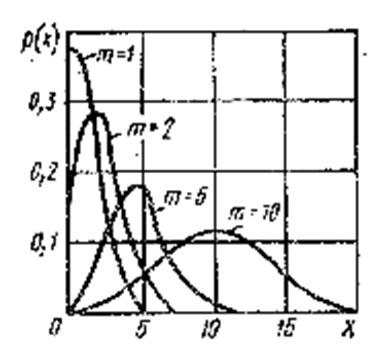
Рис.3. Общий вид кривой распределения Пуассона

Распределение Пуассона относят к редким событиям, т.е. 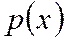- вероятность того, что событие в период какого-то испытания произойдет х раз при очень большом числе измерений т. Для закона Пуассона дисперсия равна математическому ожиданию числа наступления события за время 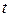, т.е. 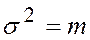. Пуассоновский процесс можно задать параметрами х и т.

Для исследования количественных характеристик некоторых процессов можно применять показательный закон распределения (рис.4, а). Плотность вероятности показательного закона выражается зависимостью 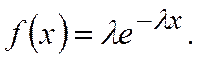Здесь плотность является величиной, обратной математическому ожиданию 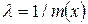, кроме того,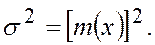

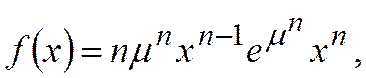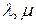В различных областях исследований широко применяется закон распределения Вейбулла (рис.4, б) где - параметры закона; 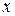- аргумент.

Исследуя процессы, связанные с постепенным снижением параметров, применяют закон 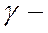распределения (рис.4, в)

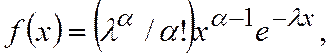
где - параметры. Если 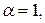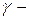функция превращается в показательный закон.

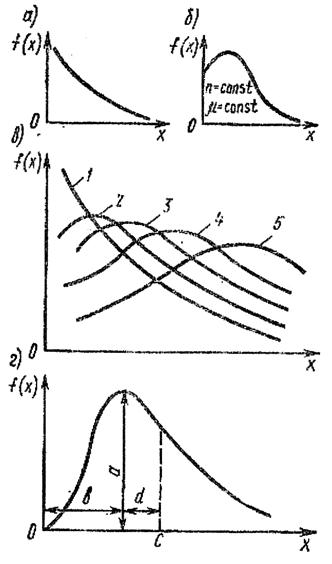
Рис.4. Кривые распределения:

При исследований многих процессов, связанных с установлением расчетных характеристик, материалов и т.п., используют закон распределения Пирсона (рис.4, г), чаще всего представляемый в виде

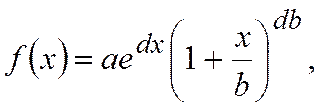
где а - максимальная ордината; d, b - соответственно расстояния от максимальной ординаты до центра распределения С и начала координат О.

Дата добавления: 2014-01-07