Результаты измерений прочности грунта методом пенетрации и их обработка

Критерий воспроизводимости (Кохрена).

Ответственные эксперименты должны быть проверены также и на воспроизводимость результатов, т.е. на их повторяемость в определенных пределах измерений с заданной доверительной достоверностью. Суть такой проверки сводится к следующему. Имеется несколько параллельных опытов (серий). Для каждой серии вычисляют среднеарифметическое значение 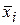(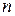- число измерений в одной серии, принимаемое обычно равным 3...4). Далее вычисляют дисперсию 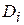. Чтобы оценить воспроизводимость, рассчитывают критерий Кохрена (расчетный):

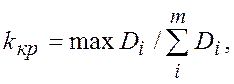
где 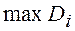- наибольшее значение дисперсий из числа рассматриваемых параллельных серий т; 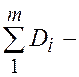сумма дисперсий т серий. Рекомендуется принимать 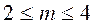. Опыты считают воспроизводимыми при

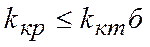
где 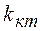- табличное значение критерия Кохрена (табл.1), принимаемое в зависимости от доверительной вероятности 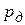и числа степеней свободы . Здесь т - число серий опытов; n - число измерений в серии.

Таблица 1

Критерий Кохрена при 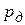= 0,95

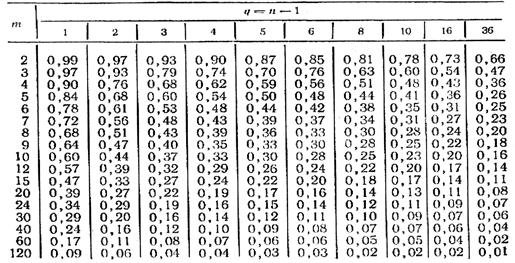
m - число параллельных серий опытов;

q - число степеней свободы;

n - число измерений в серии

Пусть, например, проведено три серии опытов по измерению прочности грунта методом пенетрации (табл.2). В каждой серии выполнялось по пять измерений (повторностей). Тогда

Вычислим число степеней свободы q = n – 1 = 5 – 1 = 4. Так, например, для 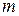= 3 и = 4 согласно табл.1 значение критерия Кохрена = 0,74. Так как 0,55 < 0,74, то измерения в эксперименте следует считать воспроизводимыми. Если бы оказалось наоборот, т.е. 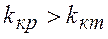, то необходимо было бы увеличить число серий 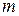или число измерений п.

Таблица 2

20. Регрессионный анализ.

Под регрессионным анализом понимают исследование закономерностей связи между явлениями (процессами), которые зависят от многих, иногда неизвестных, факторов. Часто между переменными x и у существует связь, но не вполне определенная, при которой одному значению x соответствует несколько значений (совокупность) y. В таких случаях связь называют регрессионной. Таким образом, функция 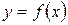является регрессионной (корреляционной), если каждому значению аргумента соответствует статистический ряд распределения у. Следовательно, регрессионные зависимости характеризуются вероятностными или стохастическими связями. Поэтому установление регрессионных зависимостей между величинами y и x возможно лишь тогда, когда выполнимы статистические измерения.

Статистические зависимости описываются математическими моделями процесса, т.е. регрессионными выражениями, связывающими независимые значения x (факторы) с зависимой переменой у (результативный признак, функция дели, отклик). Модель по возможности должна быть простой и адекватной. Например, модуль упругости материала Е зависит от его плотности 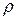так, что с возрастанием плотности модуль упругости материала увеличивается. Но выявить эту закономерность можно только при наличии большого количества измерений, так как при исследованиях каждой отдельной парной связи в зависимости 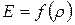наблюдаются большие отклонения.

Суть регрессионного анализа сводится к установлению уравнения регрессии, т.е. вида кривой между случайными величинами (аргументами x и функцией у), оценке тесноты связей между ними, достоверности и адекватности результатов измерений.

Чтобы предварительно определить наличие такой связи между x и у, наносят точки на график и строят так называемое корреляционное поле (рис.1). По тесноте группирования точек вокруг прямой или кривой линии, по наклону линии можно визуально судить о наличии корреляционной связи. Так, из рис.1,а видно, что экспериментальные данные имеют определенную связь между x и у, а измерения, приведенные на рис.1, б, такой связи не показывают.

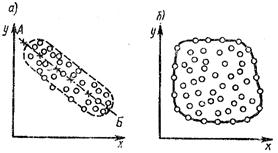
Рис.1. Корреляционное поле

Корреляционное поле характеризует вид связи между x и у. По форме поля можно ориентировочно судить о форме графика, характеризующего прямолинейную или криволинейную зависимости. Даже для вполне выраженной формы корреляционного поля вследствие статистического характера связи исследуемого явления одно значение x может иметь несколько значений у. Если на корреляционном поле осреднить точки, т.е. для каждого значения определить 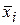и соединить точки 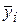, то можно будет получить ломаную линию, называемую экспериментальной регрессионной зависимостью (линией). Наличие ломаной линии объясняется погрешностями измерений, недостаточным количеством измерений, физической сущностью исследуемого явления и др. Если на корреляционном поле провести плавную линию между 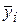, которая равноудалена от них, то получится новая теоретическая регрессионная зависимость - линия АБ (рис.1, а).

Различают однофакторпые (парные) и многофакторные регрессионные зависимости. Парная регрессия при парной зависимости может быть аппроксимирована прямой линией, параболой, гиперболой, логарифмической, степенной или показательной функцией, полиномом и др. Двухфакторное поле можно аппроксимировать плоскостью, параболоидом, гиперболоидом. Для переменных факторов связь может быть установлена с помощью 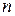-мерного пространства уравнениями второго порядка:

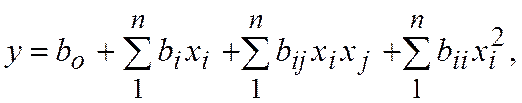
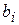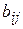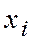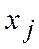где у - функция цели (отклика) многофакторных переменных; - независимые факторы; - коэффициенты регрессии, характеризующие влияние фактора на функцию цели; - коэффициенты, характеризующие двойное влияние факторов и на функцию цели.

При построении теоретической регрессионной зависимости оптимальной является такая функция, в которой соблюдаются условия наименьших квадратов min, где 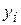- фактические ординаты поля; у - среднее значение ординаты с абсциссой x. Поле корреляции аппроксимируется уравнением прямой 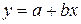. Линию регрессии рассчитывают из условий наименьших квадратов. При этом кривая АБ (рис.1) наилучшим образом выравнивает значения постоянных коэффициентов 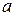и 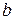, т.е. коэффициентов уравнения регрессии. Их вычисляют по выражениям

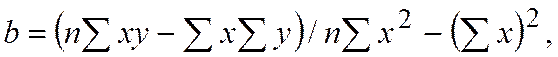
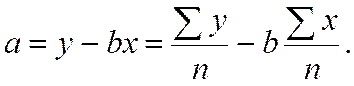
Критерием близости корреляционной зависимости между 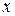и 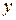к линейной функциональной зависимости является коэффициент парной или просто коэффициент корреляции 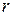, показывающий степень тесноты связи x и у и определяемый отношением

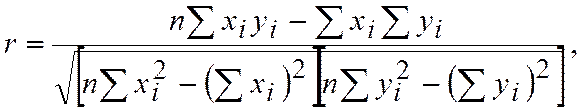
где 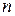- число измерений. Значение коэффициента корреляции всегда меньше единицы. При 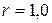x и у связаны функциональной связью (в данном случае линейной), т.е. каждому значению x соответствует только одно значение у. Если 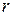<1, то линейной связи не существует. При линейная корреляционная связь между x и у отсутствует, но может существовать нелинейная регрессия. Обычно считают тесноту связи удовлетворительной при 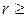0,5; хорошей при 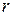= 0,8 - 0,85. Для определения процента разброса (изменчивости) искомой функции y относительно ее среднего значения, определяемого изменчивостью фактора x, вычисляют коэффициент детерминации

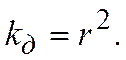
Уравнение регрессии прямой можно представить выражением

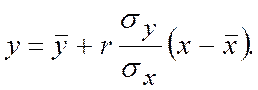
Пусть, например, имеется статистический ряд парных измерений:

по которому можно найти уравнение прямолинейной регрессии, оценить тесноту связей и оценить степень достоверности. Расчет целесообразно вести в табличной форме (табл.1).

В табл.1 приведена сходимость экспериментальной и теоретической регрессии:

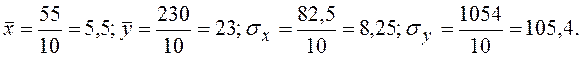
Таблица 1

Расчет уравнения регрессии

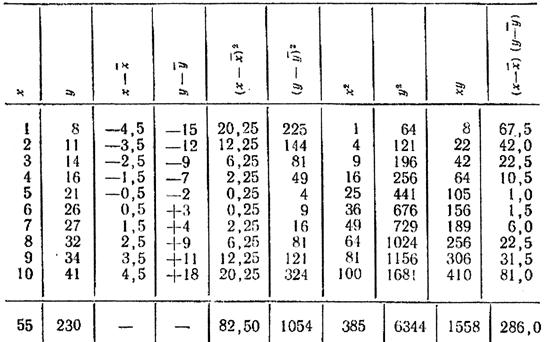
Таблица 2

Сходимость экспериментальной и теоретической регрессии

Коэффициент корреляции

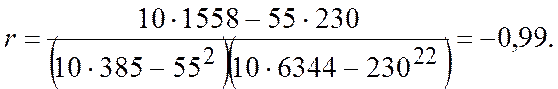
Коэффициенты будут

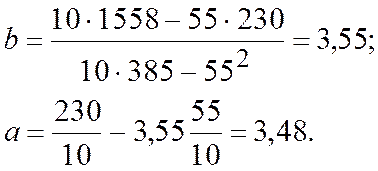
Уравнение регрессии имеет вид

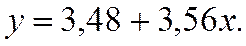
Как видно из расчетов, сходимость оказалась хорошей.

Коэффициент детерминации составляет 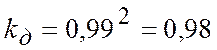, что означает, что 98 % разброса определяется изменчивостью, а 2 % - другими причинами, т.е. изменчивость функции у почти полностью характеризуется разбросом (природой) фактора .

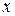На практике часто возникает потребность в установлении связи между у и многими параметрами 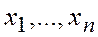на основе многофакторной регрессии.

Миогофакторные теоретические регрессии аппроксимируются полиномами первого или второго порядка. Математические модели характеризуют стохастический процесс изучаемого явления, уравнение регрессии определяет систематическую, а ошибки разброса - случайную составляющие.

Теоретическую модель множественной регрессии можно получить методами математического планирования, т.е. активным экспериментом, а также пассивным, когда точки факторного пространства выбираются в процессе эксперимента произвольно.

21. Критерий Фишера.

В результате эксперимента получают статистический ряд обычно парных, однофакторных 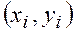или многофакторных измерений. Статистические измерения подвергают обработке и анализу, подбирают эмпирические формулы и устанавливают их достоверность.

Перед подбором эмпирических формул необходимо еще раз убедиться в достоверности эксперимента, окончательно проверить воспроизводимость результатов по критерию Кохрена. Оценка пригодности гипотезы исследования, а также теоретических данных на адекватность, т.е. соответствие теоретической кривой экспериментальным данным, необходима во всех случаях на стадии анализа теоретико-экспериментальных исследований. Методы оценки адекватности основаны на использовании доверительных интервалов, позволяющих с заданной доверительной вероятностью определять искомые значения оцениваемого параметра. Суть такой проверки состоит в сопоставлении полученной или предполагаемой теоретической функции 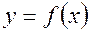c результатами измерений. В практике оценки адекватности применяют различные статистические критерии согласия.

Одним из таких критериев является критерий Фишера. Установление адекватности - это определение ошибки аппроксимации опытных данных. Для этого необходимо рассчитать экспериментальное (опытное) значение критерия Фишера 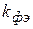и сравнить его с теоретическим (табличным) 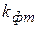, принимаемым при требуемой доверительной вероятности 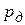(обычно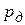= 0,95). Если модель адекватна; если 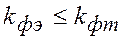модель неадекватна. Опытный критерий Фишера вычисляют по формуле

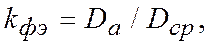
где - дисперсия адекватности; 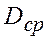- средняя дисперсия всего эксперимента, определяющиеся как

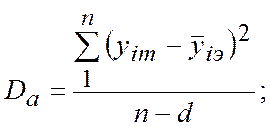
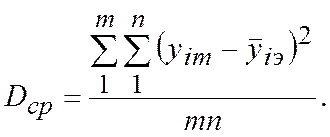
Здесь 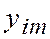- теоретическое значение функции для каждого измерения; 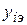- экспериментальное значение функции; 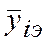- среднее экспериментальное значение функции из m серий измерений; п - количество измерений в одном опыте (одной серии или количество опытов); d - число коэффициентов уравнения теоретической регрессии.

Значение 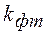принимается по табл. для доверительной вероятности 0,95 и числа степеней свободы 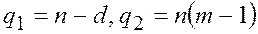. Величину 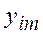вычисляют по теоретической регрессии для фактора 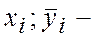как средние из т серий измерений, т.е.

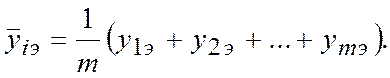
Таблица

Дата добавления: 2014-01-07