Что позволяет записать

Интегрирование последнего уравнения в пределах от нуля до дает

Или

.

,

.

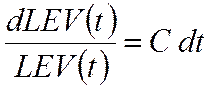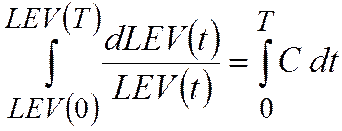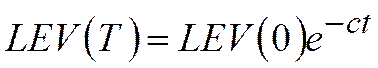Постоянная времени 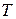, за которое уровень возрастает в 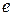раз имеет значение 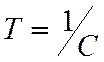. Эта величина характеризует скорость роста в системе с положительной связью. Время, за которое значение уровня увеличивается вдвое, равно

.

Положительная обратная связь характеризуется целенаправленным поведением (рис.5). В этом случае темп потока зависит от разности между фактическим и желаемым состоянием системы. Цель определяется экзогенно.

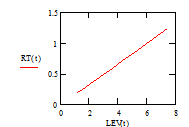
Рис.4. Решение разностного уравнения:

а – динамика уровня LEV(t); б – динамика темпа RT(t);

в – взаимосвязь между уровнем LEV и темпом RT;

C₁ = 0,2; LEV(0) = 1; t = 0…10

Модель описывается системой уравнений

; (2.9)

, (2.10)

где – константа пропорциональности;

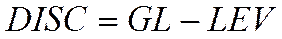– разность между уровнем и целью.

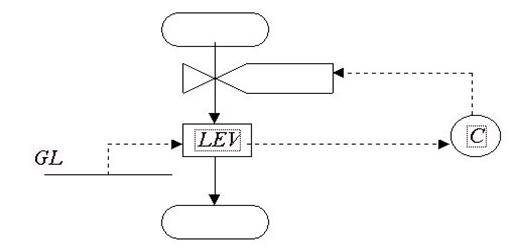
Рис.5. Схема контура с отрицательной обратной связью

Подстановка позволяет переписать систему в виде

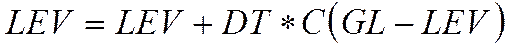
или с учетом предельного перехода

.

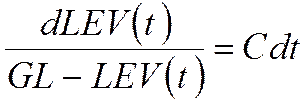Интегрирование в пределах от нуля до 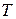дает

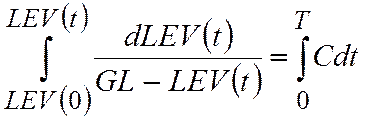
или

.

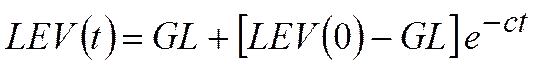За характерное время 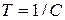уровень увеличивается на величину 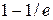от разности между целью и достигнутым значением уровня

.

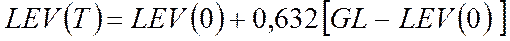Система достигает цели за время равное примерно 3T. Уровень при этом составляет 0,95GL.

Уточнение связей между отдельными подсистемами и образуемыми ими эшелонами требует дальнейшего исследования, и может быть произведено, например, аналитическим методом.

Эшелоны региональной системы агропромышленного комплекса охвачены информационными связями, которые определяются междуэшелонными множителями. В случае, когда к подсистеме присоединяется одна информационная связь, множитель определяется отношением величины темпа, в который она входит, к величине уровня, из которого она исходит. Например, в случае подсистемы плотности населения региона множитель PKPP отношению темпа роста плотности населения PPG к уровню численности сельского населения PK.

Определение множителей влияния при связи темпа подсистемы с двумя и более уровнями других подсистем может быть выполнено на основе определения частных производных в конечных разностях.

В качестве примера рассмотрим подсистему численности сельского населения PK. Системные связи от уровня качества жизни QL и уровня капиталовложений (фондов) в сельском хозяйстве KI определяются действием множителей QLPK и KIPK на темп роста сельского населения PKG.

Представим эту связь в виде конечных приращений

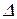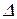QLPK = PKG/QL,

где QLPK – степень влияния качества жизни на численность сельского населения;

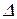PKG = .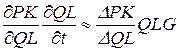

В приведенных соотношениях дифференциалы уровне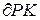й и 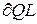заменены конечными приращениями и .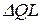

После подстановки конечного приращения темпа 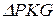получим

QLPK = .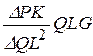

Подстановка численных значений дает

QLPK = 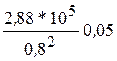= 2,25.10⁴ чел./(ед. год).

Аналогично определяются и остальные множители системы.

Дата добавления: 2014-01-07