Синхронной машины

УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПЕРЕХОДНОГО ПРОЦЕССА

Лекция 7

Переходный процесс в электрической машине может быть описан системой дифференциальных уравнений. Выбор системы координат определяется конкретными условиями решаемой задачи.

Дифференциальные уравнения равновесия ЭДС и падений напряжений в каждой из обмоток статора (А, В, С) и ротора (f):

U _А = - 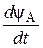- R _А i _А;

U _В = - 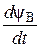– R _В i _В;

U _С = - – R _С i _С;

U_f = 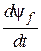+ R_fi_f,

где R _А, R _В, R _С, R_f – активные сопротивления контуров фаз А, В, С и обмотки возбуждения; Ψ_А, Ψ_В, Ψ_С, Ψ _f - результирующие потокосцепления контуров фаз А, В, С и обмотки возбуждения.

Потокосцепление обмотки фазы А выражается уравнением:

Ψ_А = L _А i _А + M _АВ i _В + M _АС i _С + M _{А f}i_f,

Ψ_В = M _ВА i _А + L _В i _В + M _ВС i _С + M _{В f}i_f,

Ψ_С = M _СА i _А + M _СВ i _В +L _С i _С + M _{С f}i_f,

Ψ_f = M _fA i _A + M _fB i _B + M _fC i_C + L _f i _f,

где L _А, L _В, L _С, – коэффициент самоиндукции обмотки фаз А, В, С; M _АВ, M _ВА, M _СА, M _СВ, M _СА, M _ВС, - коэффициент взаимоиндукции обмоток фаз А, В и С; M _{А f} - коэффициент взаимоиндукции обмотки фазы А и обмотки возбуждения.

Во вращающейся машине коэффициенты L и M не являются постоянными коэффициентами и зависят от положения ротора относительно обмоток статора и, следовательно, являются функциями времени.

Закон изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора выражается синусоидальной функцией.

М_Аf = М_fА = М_Аfсоsγ

где γ – угол между магнитной осью фазы А и продольной осью ротора d.

Индуктивность обмотки фазы А определяют как

L_А = l₀ + l₂соs2γ

Взаимная индуктивность М_АВ = m₀ + m₂соs2(γ - π/3)

где l₀ и m₀ – постоянные составляющие соответствующих индуктивностей;

l₂ и m₂ – амплитуды вторых гармоник тех же индуктивностей.

Коэффииценты l₀ и m₀ и l₂можно выразить через индуктивности, которыми характеризуется синхронная машина

l₀ = 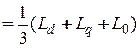; l₂ = ;

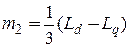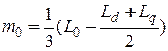
Систему дифференциальных уравнений с переменными коэффициентами решить очень сложно. Для её решения существуют несколько способов. Мгновенные значения фазных величин (U, Ψ, i) можно получить как проекции фазных векторов на неподвижную ось времени t или как проекции обобщенного вектора f на неподвижные магнитные оси фаз А, В и С. Вектор f в общем случае может характеризовать фазные величины, изменяющиеся во времени по произвольному закону. Представление трехфазной системы векторов обобщенным вектором упрощает выражение связи между статором и ротором, что позволяет в дифференциальных уравнениях переходного процесса освободится от переменных коэффициентов.

Дата добавления: 2014-01-07