Однократная поперечная несимметрия

ЛЕКЦИЯ 13

Основные уравнения второго закона Кирхгофа отдельно для каждой последовательности

где- симметричные составляющие напряжения и тока в месте короткого замыкания; 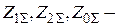результирующие сопротивления схем соответствующих последовательностей относительно точки короткого замыкания.- результирующая ЭДС относительно точки короткого замыкания.

Так как токи и напряжения обратной и нулевой последовательностей пропорциональны току прямой последовательности I _к1, то расчет сводится к нахождению тока I _к1. Ток прямой последовательности любого несимметричного КЗ можно выразить как

= ,

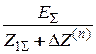где E _S - результирующая ЭДС схемы прямой последовательности; Z _1S - результирующее сопротивление прямой последовательности; D Z ^{( n )} - дополнительное сопротивление, определяемое значениями результирующих сопротивлений обратной Z _2S и нулевой Z _0S последовательностей. Величина дополнительного сопротивления D Z ^{( n )} для различных видов КЗ:

Однофазное.................................................................................. Z _1S + Z _2S

Двухфазное.............................................................................................. Z _2S

Двухфазное на землю.................................................................... Z _2S / Z _0S

Правило эквивалентности прямой последовательности: ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительное сопротивление D Z ^{( n )}, определяемое видом КЗ. Выражения для определения симметричных составляющих токов и напряжений в точке КЗ, а также токов и напряжений фаз приведены в табл. 3.1.

Модуль фазного тока любого (n) несимметричного КЗ в общем виде может быть выражен через ток прямой последовательности как

= m ^{( n )} ,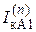

где m ^{( n )} - коэффициент, зависящий от вида короткого замыкания.

При неучете активных сопротивлений в схеме величина коэффициента m ^{( n )} для различных видов КЗ приведена ниже:

Однофазное..................................................................................................... 3

Двухфазное....................................................................................................

Двухфазное на землю........................................

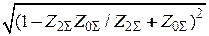
При расчете токов при несимметричных коротких замыканиях составляются схемы замещения отдельных последовательностей. В схему замещения прямой последовательности генераторы, крупные синхронные и асинхронные двигатели вводятся своими сверхпереходными параметрами. Схемы преобразуются к простейшему радиальному виду и определяются эквивалентные ЭДС E _S и сопротивления Z _1S, Z _2S, Z _0S,. По правилу эквивалентности прямой последовательности определяются симметричные составляющие сверхпереходного тока в точке КЗ и его полное значение. Далее определяют симметричные составляющие токов во всех ветвях схемы.

Проходя через трансформатор со стороны “звезды” на сторону “треугольника” токи и напряжения изменяются как по величине, так и по фазе в зависимости от схемы соединения обмоток. Ток в линейном проводе за “треугольником” фазы А I _а определяется по выражению

I _а = I _А1е ^{j 30° N} + I _А2е^{- j 30° N},

где N - номер группы соединения обмоток трансформаторов в соответствии с правилом часового циферблата; I _а - ток фазы А со стороны обмотки трансформатора, соединенной в “треугольник”; I _А1, I _А2 - симметричные составляющие тока фазы А со стороны обмотки трансформатора, соединенной в “звезду”.

Расчетные значения симметричных составляющих токов и напряжений приведены в табл.1.

Таблица 1 Расчетные значения симметричных составляющих

токов и напряжений

№	Обозначения и определяемые величины	Вид короткого замыкания
	Однофазное	двухфазное	Двухфазное на землю
	Ток обратной последовательности I кА2	I кА1	- I кА1	- I кА1 Z 0S/(Z 2S + Z 0S)
	Ток нулевой последовательности I кА0	I кА1		- I кА1Z2S/(Z 2S + Z 0S)
	Напряжение прямой последовтельности U кА1	I кА1(Z 2S + Z 0S)	I кА1 Z 2S	I кА1 Z 2S Z 0S/(Z 2S + Z 0S)
	Напряжение обрат-ной последовательности U кА2	- I кА1 Z 2S	- I кА1 Z 2S	I кА1 Z 2S Z 0S/(Z 2S + Z 0S)
	Напряжение нулевой последовательности U кА0	- I кА1 Z 0S		I кА1 Z 2S Z 0S/(Z 2S + Z 0S)
	Ток в фазе “А” I кА	3 I кА1
Ток в фазе “В” I кВ		j Ö3 I кА1	{а^2- [(Z 2S + а Z 0S)/ (Z 2S + Z 0S)]} I кА1
Ток в фазе “С” I кС		- j Ö3 I кА1	{а- [(Z 2S + а^2 Z 0S)/ (Z 2S + Z 0S)]} I кА1
	Напряжение U кА		Z 2S I кА1	3 I кА1 Z 2S Z 0S/(Z 2S + Z 0S)
Напряжение U кВ	[(а^2-а) Z 2S + (а^2-1) Z 0S] I кА1	-2 Z 2S I кА1
Напряжение U кС	[(а - а^2) Z 2S + (а-1) Z 0S] I кА1	-2 Z 2S I кА1

Ударный коэффициент рассчитывается по формуле

К_у = 1 + ,

где Т _э = (Х _1S + D Х ^{( n )})/314(R _1S + D R ^{( n )}) - эквивалентная постоянная времени, с; D Х ^{( n )}, D R ^{( n )}- дополнительные индуктивное и активное сопротивления, определяемые видом КЗ.

Расчетные схемы отдельных последовательностей для установившегося режима составляются аналогично как и для расчета начального режима, только вместо начальных параметров вводятся параметры элементов установившегося режима. Схемы преобразуются к простейшим радиальным, определяются эквивалентные параметры, симметричные составляющие и полные токи фаз в месте КЗ. Далее определяют токи во всех ветвях схемы.

При учете АРВ генераторов расчет несимметричного режима аналогичен расчету симметричного с учетом сопротивлений D Х ^{( n )}, D R ^{( n )}.

Типовые кривые могут быть использованы для определения тока прямой последовательности в произвольный момент процесса любого несимметричного КЗ. Расчет производится аналогично расчету симметричного режима КЗ, но с учетом дополнительного сопротивления D Х ^{( n )}. Для этого нужно предварительно найти реактивность схемы прямой последовательности, в которой точка КЗ должна быть отнесена на дополнительное сопротивление D Х ^{( n )}. По расчетной схеме и по типовым кривым определяется ток прямой последовательности. Полный ток в точке КЗ определяется как

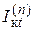= m ^{( n )},

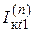где 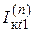- ток прямой последовательности для момента времени t.

Порядок расчета несимметричных токов КЗ:

1) составляют схемы замещения отдельных последовательностей;

2) находят результирующие сопротивления отдельных последовательностей относительно точки КЗ и результирующую ЭДС прямой последовательности относительно той же точки;

3) в соответствии с комплексной схемой замещения для конкретного вида КЗ определяют ток прямой последовательности;

4) по основным кривым находят для интересующего момента времени искомый ток в месте КЗ;

5) определяют значения полных токов и напряжений фаз в месте КЗ, в ветвях и узлах схемы для интересующего момента времени, учитывая при этом группы соединения обмоток силовых трансформаторов.

Тема для самостоятельной проработки -Комплексные схемы замещения при однократной продольной несимметрии

Литература: [1], § 14 - 1 – 14.14;

[2], § 10.3 - 10.4;

[3], § 2 - 20, 2 - 21;

[4], § 6 - 7, 6 - 8.

Дата добавления: 2014-01-07