Численное решение нелинейных уравнений и систем

6.1 Отделение корней

Одна из простейших задач, часто возникающая при математическом моделировании различных систем, – нахождение приближенных значений корней нелинейных уравнений и трансцендентных уравнений, например .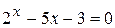

Всякое нелинейное алгебраическое или трансцендентное урав­нение с одним неизвестным может быть записано в виде

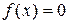(1)

где 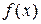- функция вещественного переменного.

Решением (или корнем) уравнения (1) называется такое зна­чение 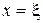, при котором функция 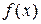обращается в нуль, т. е. .

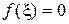Корень 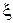уравнения (1) называется простым, если 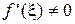. В противном случае (т.е. 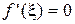) корень 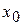называ­ется кратным. Целое число т назовем кратностью корня 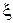, ес­ли 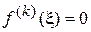для значени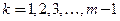й и .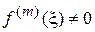

Вещественный корень уравнения (1) геометрически пред­ставляет абсциссу точки пересечения или касания графика функции 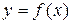и оси Ох.

Функция 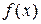(график которой изображен на рисунке) имеет четыре корня. Корн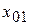и и 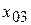- простые, 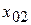и 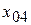- кратные. Ес­ли какой-либо вещественный корень является двукратным, напри­мер, 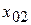то кривая 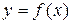касается оси Ох в точке, где .

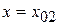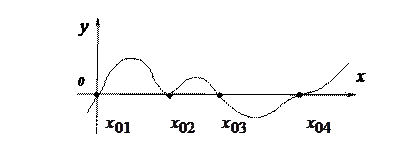
Рис. 1. Простые и кратные корни уравнения (1)

Задача отыскания простых корней является существенно более простой (и чаще встречающейся), чем задача отыскания кратных корней. В действительности большинство методов решения урав­нения (1) ориентировано именно на вычисление простых кор­ней.

Процесс нахождения приближенных значений корней нелиней­ного уравнения осуществляется в два этапа. Первый этап называет­ся этапом локализации (или отделения) корней, второй - эта­пом уточнения корней до заданной степени точности.

Корень 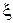уравнения (1) считается отделенным (или лока­лизованным) на отрезке 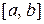, если на этом отрезке уравнение (1) не имеет других корней.

Отрезок 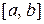, содержащий только один корень 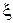уравнения (1), называют отрезком локализации корня 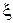(его длину стараются по возможности сделать минимальной).

Отделить корни - это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень. Отделение корней можно произвести графическим методом, если построить график функции 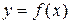. Точки пересечения графика с осью Ох дают значения корня, и по графику легко определить два числа а и b, между которыми заключен только один корень.

Пример. Определить графически, между какими целыми числами заключены корни уравнения 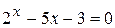. Построим график функции и определим абсцис­сы точек пересечения этого графика с осью Ох (рис. 1.). Кривая пересекает ось Ох в двух точках; следовательно, уравнение имеет два вещественных корня. Из чертежа видно, что корни принадлежат отрезкам , .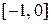

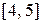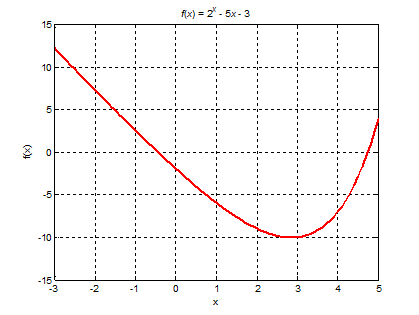
Рис. 2. Графический метод отделения корней

Графический метод отделения корней не обладает большой точ­ностью. Он дает возможность грубо определить интервалы изоля­ции корня. Далее корни уточняют одним из способов, указанных ниже.

Предположим, что 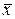— приближенное значение корня, 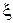— его точное значение. Возникает вопрос, какова погрешность 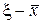приближенного значения корня 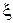по сравнению с его точ­ным значением 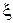, если последний неизвестен?

Для этого построим невязку 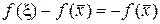, т. к. 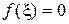. Применим к невязке теорему Лагранжа о конечных прира­щениях:

,

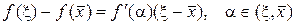откуда

.

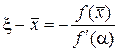Так как точное значение 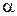неизвестно, эту погрешность за­меняют верхней оценкой:

. (*)

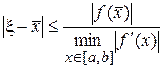Оценка погрешности (*) является довольно грубой. Поэто­му в каждом итерационном методе уточнения корней, в силу ограничений применения метода, можно вывести свою оценку погрешности.

6.2 Метод деления пополам. (Метод бисекций)

Пусть требуется с заданной точностью 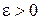найти корень 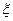уравнения

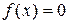. (1)

Отрезок локализации 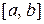(т. е. отрезок, содержащий только один корень 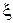) будем считать заданным, причем 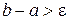. Предполо­жим, что функция 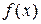непрерывна на отрезке 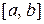и на его кон­цах принимает значения разных знаков, т. е. 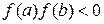. В основе метода лежит следующая теорема:

Теорема (Больцано-Коши о промежуточном значении). Ес­ли функция 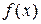, непрерывная на отрезке 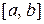, принимает на его кон­цах значения разных знаков, т. е. 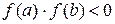, то на отрезке есть точка, в которой функция обращается в нуль.

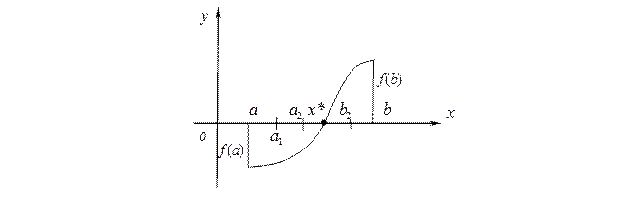
Рис. 3. Метод деления пополам

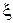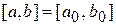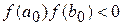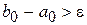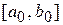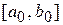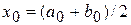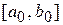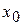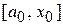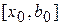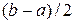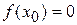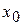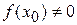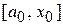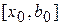Пусть корень уравнения (1) отделен и находится на от­резке (и ). Возьмем на отрезке промежуточную точку, так, чтобы она являлась серединой отрезка , т. е. . Тогда отрезок точкой разделится на два рав­ных отрезка и . Длина каждого отрезка равна . Если , то - точный корень уравнения (1). Если же , то из двух полученных отрезков и выберем тот, на концах которого функция 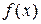принимает значению проти­воположных знаков; обозначим его 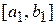. Затем отрезок 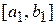также делим пополам и проводим те же рассуждения. Получим от­резок 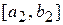, длина которого равна 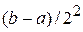. Процесс деления от­резка пополам производим до тех пор, когда на каком-то к- ом этапе либо середина отрезка окажется корнем уравнения (случай, весьма редко встречающийся на практике), либо получится отрезок 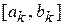такой, что

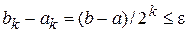(2)

и 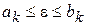(число к указывает на количество проведенных делений). Числа 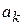и 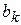- корни урав­нения (1) с точностью до значения 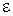. За приближенное значе­ние корня, следует взять .

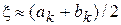Из неравенства (2) можно оценить число итераций необходимых для достижения заданной точности (априорная)

.

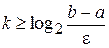Достоинства:

а) метод половинного деления прост в алгоритмизации и про­граммировании;

б) на функцию 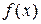не накладывается никаких ограничений,
кроме требования непрерывности.

Недостаток: метод очень медленно сходится, т.е. необ­ходимо использовать большое число итераций для достижения заданной точности .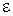

6.3 Метод простых итераций

Пусть требуется с заданной точностью 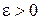найти корень 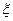уравнения

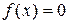. (1)

Отрезок локализации 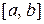будем считать заданным, причем 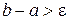. Предположим, что функция 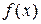непрерывна на отрезке .

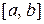Заменим уравнение (1) эквивалентным ему уравнением вида

. (2)

Это преобразование (приведение уравнения к виду, удобному для итерации) можно выполнить различными способами; некоторые из них будут указаны ниже. Функцию 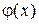далее будем называть итерационной функцией.

Выберем каким-либо образом в качестве начального приближе­ния какое-либо значение 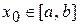, например 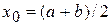, (или графически или методом бисекций). Затем вычислим 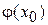, и по­лученное число 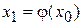примем за первое приближение зна­чения корня 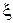. Подставив 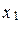вместо 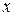в правую часть уравнения (2), получим новое число 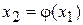. Продолжая этот процесс неограниченно, получим последовательность приближений к корню 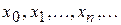определяемых следующими соотношениями

;

;

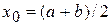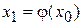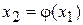; (3)

…

.

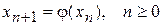Если не удается выразить 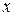из уравнения (1), то эквивалентное уравнение и эквивалентную функцию можно построить, например, так

, .

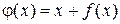Последовательность (3) называется методом простых итераций уточнения корней уравнения (1).

Сходиться ли последовательность (3), и, если сходиться, являются ли предельное значение корнем уравнения (2), а следовательно, и уравнения (1)? Имеет место теорема.

Теорема (достаточные условия сходимости метода простых итерации). Пусть функция 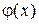в эквивалентном уравнении (2) определена и дифференцируема на отрезке 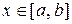. Тогда, если существует число q такое, что

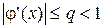(4)

на отрезке 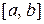, то последовательность (3) сходится к един­ственному корню уравнения (2) при любом начальном прибли­жении .

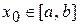На практике итерационный процесс останавливают при выполне­нии условия

, .

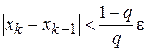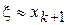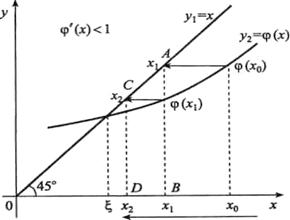
Рис. 4. К методу простых итераций в случае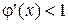

Геометрическая интерпретация метода простых ите­раций. Из рис. 4. видно, что 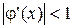, так как тангенс угла наклона касательной к графику функции 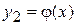мень­ше tg(45°) = 1. Следовательно, для произвольного начального приближения 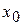в соответствии с 1-й итерацией в (3) при 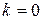определяется 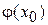, которое равно значению 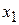на графике функции 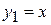, а поскольку треугольник ОАВ прямоугольный и равнобедренный, то ОВ = 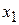. На следующей итерации в (3) при 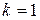определяется 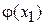, которое равно значению 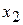на графике функции 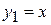, а поскольку треугольник OCD — равнобедрен­ный и прямоугольный, то CD = OD = 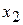, т.е. итерационные значения 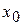, , 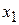,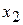…. стремятся в сторону точного корня 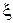(указано стрелкой справа налево).

На рис. 5. 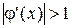. Из рисунка видно, что итерационный процесс расходится (приближения корня 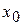, , 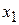,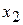…. стремят­ся от корня ).

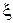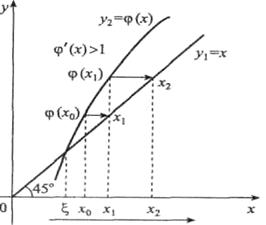  Рис. 5. К методу простых итераций в случае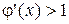

На рис. 6. представлен случай 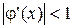, 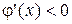. Про­цесс итераций сходится с двух сторон, т. е. приближения корня находятся то слева, то справа от точного корня .

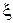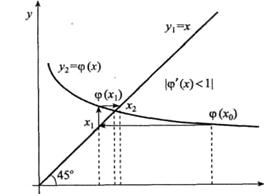
Рис. 6. К методу простых итераций в случае ,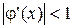

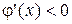
Исходное уравнение всегда можно привести к виду удобному для итераций. Для этого вернемся к исходному уравнению (1) и построим эквивалентное уравне­ние в виде

,

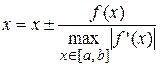где берется знак минус, если 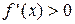, и плюс, если .

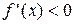Тогда в качестве эквивалентной функции 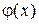можно при­нять функцию

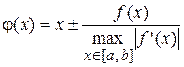
для которой

.

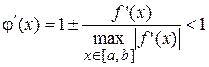6.4 Метод Ньютона

Пусть для урав­нения

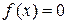(1)

на интервале 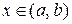отделен корень .

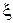Пусть имеется некоторое приближение корня точка – 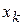. Тогда, (к + 1)-ое приближение корня будем искать в виде:

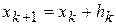, (2)

где 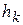– шаг, который подлежит определению.

Чтобы определить 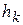, подставим разложим функцию 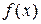в ряд Тейлора в окрестности точки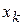

.

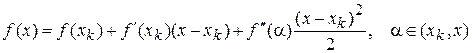Заменим в этом разложении 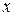на корень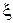

.

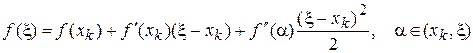Но 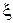– корень, так что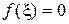

.

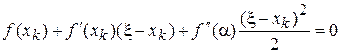Отбросим в этом разложение малое слагаемое 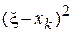. Поскольку точка 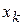близка к корню 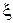, то разность 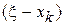по модулю мала, следовательно величина 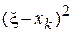будет тем более малой

.

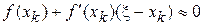Однако корнем линейного уравнения буде уже не точка 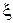, а близкая к ней точка которую обозначим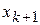

.

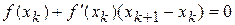Заменяя в этом уравнении разность 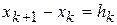, получаем

.

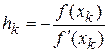Подставляем 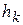в (2), получаем

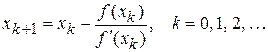(3)

Выражения (3) называют итерационным мето­дом Ньютона уточнения корней нелинейного уравнения (1). Метод Ньютона называют также методом касательных. В этом методе на каждой итерации к графику функ­ции 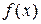проводится касательная в точке 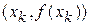до пересе­чения с осью абсцисс (рис.). Уравнение касательной имеет вид

.

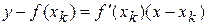Полагая в этом уравнени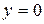и и 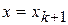, получим формулу Ньютона (3).

Справедлива следующая теорема.

Теорема (достаточные условия сходимости метода Ньютона). Пусть 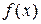определена и дважды дифференцируе­ма на отрезке 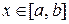, причем 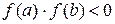, производные 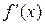и 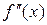знакопостоянны и 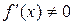. Тогда исходя из начального приближения 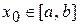, удовлетворяющего неравен­ству 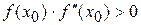, можно построить последовательность (3), сходящуюся к единственному корню 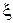уравнения (1) на отрезке 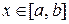с погрешностью, оцениваемой неравенством

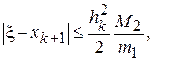(4)

где , , .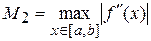

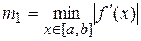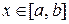Согласно теореме за начальное приближение можно принять один из концов отрезка 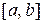, а именно

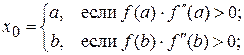(5)

Поскольку верхняя оценка (4) сложна для вычисления, на практике итерационный процесс останавливают при выполнении условия 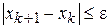, , 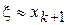где 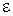— заданная точность.

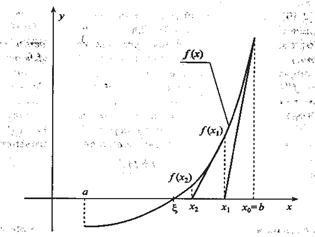
Рис. 7. Метод Ньютона

Для случая, приведенного на рисунке, за начальное прибли­жение принимается 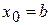, так как .

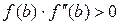Дата добавления: 2014-01-07