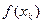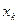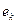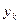Интерполяция кусочно-многочленными функциями

Задача интерполяции.

Пусть вся информация о функции ограничивается таблицей данных:

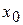
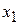
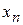
		………………..		(1)
		………………..

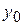
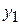
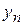
Такую функцию будем называть сеточной функцией (или табличной). Точки 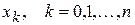– узлами сетки.

Эту информацию обычно дополняют предположение о непрерывности функции 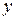между заданными точками.

Задача интерполяции заключается в том, чтобы найти аналитическую зависимость выходного параметра 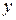от входных данных 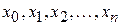в виде:

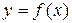, (2)

где 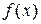- непрерывная функция, удовлетворяющая в точках таблицы 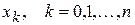равенствам

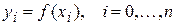. (3)

В этом случае говорят, что функция (2)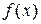 интерполирует табличную функцию (1), точки 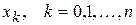называют узлами интерполяции, а условие (3) – условием интерполяции.

При сглаживании сеточной функции с помощью интерполяции в соответствии с условием (3) значение интерполирующей функции и значение заданной функции в узлах сетки должны быть одинаковыми, следовательно, погрешность интерполяции в узлах 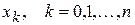равна нулю (рис. 1).

Относительно поведения непрерывной функции между табличными значениями могут быть сделаны различные предположения, поэтому существует множество методов интерполирования.

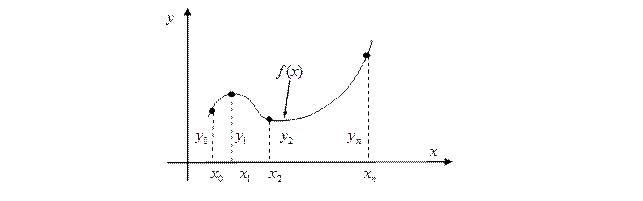
Рис. 1. Задача интерполяции

Применение интерполяционных многочленов.

Задача интерполяции имеет не единственное решение, но в одном случае, когда интерполирующей функцией является многочлен n -й степени (n + 1 число узлов интерполяции) интерполяция имеет единственное решение.

Действительно, пусть приближенная функция, является многочленом п-й степени,

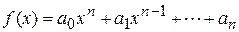, (4)

где п + 1 — число узлов в таблице (1), с неизвестными пара­метрами 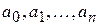. Используя таблицу (1), многочлен (4) и условие интерполяции (3), составим СЛАУ относительно неизвестных коэффициентов :

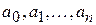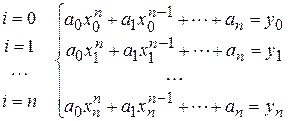(5)

Неоднородная СЛАУ (5) имеет единственное решение для коэффициентов 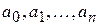, так как определитель матрицы этой СЛАУ (определитель Вандермонда) не равен нулю:

,

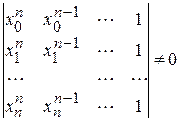поскольку все значения узлов интерполяции различны между собой и ни одна из строк не является линейной комбинацией дру­гих. Таким образом, задача многочленной интерполяции имеет единственное решение, так как коэффициенты 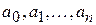могут быть выбраны единственным образом.

Интерполяционный многочлен Лагранжа.

Для многочленной интерполяции можно и не решать СЛАУ (5), а многочлен (4) можно составить следующим образом.

Запишем систему многочленов n -й степени:

,

………………………………………………………………

.

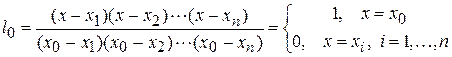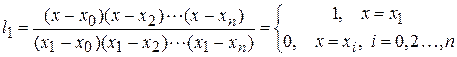
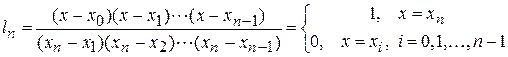Составим линейную комбинацию этих многочленов (их коли­чество равно п + 1) с коэффициентами линейной комбинации, равными значениям 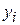сеточной функции (1), получим много­член п-й степени

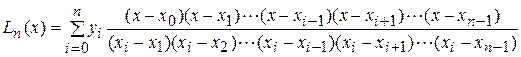. (6)

Многочлен (6) называют интерполяционным многочленом Лагранжа n -й степени, так как он, во-первых, удовлетворяет условию интерполяции

,

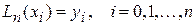и, во-вторых, имеет n -ю степень.

Интерполяционный многочлен Лагранжа обладает тем недо­статком, что в случае, когда добавляются новые узлы интерполя­ции в таблице (1), все слагаемые в (6) необходимо пересчиты­вать. Но, с другой стороны, он обладает тем достоинством, что интервалы между узлами могут быть неравномерными:

.

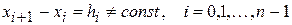Выпишем наиболее употребляемые многочлены 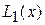и .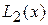

1) Для таблицы с двумя узлами интерполяции :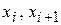

		;

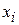
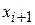
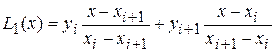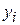
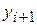
2) Для таблицы с тремя узлами интерполяции :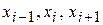

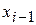
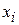
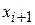
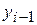
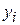
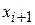
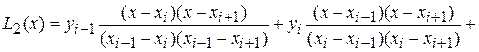
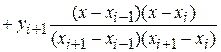
Интерполяционный многочлен Ньютона.

Рассмотрим случай равностоящих значений аргумента, т.е.

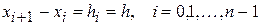
и введем понятие конечных разностей. Конечной разностью первого порядка сеточной функции (1) в узле 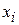называют разность

.

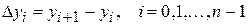Конечной разностью второго порядка сеточной функции (1) в узле 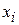называют разность первого порядка от разности первого порядка:

,

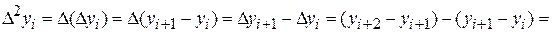
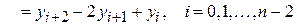и т.д., конечная разность к- го порядка в узле 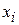равна

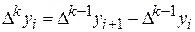
и может быть выражена непосредственно через значения функции.

Конечной разностью сеточной функции нулевого порядка в узлах 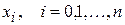, являются значения 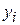этой функции в этих узлах.

Конечные разности удобно размещать в одну общую таблицу с узлами и значениями функции. Эту таблицу называют таблицей конечных разностей:

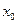
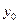
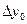
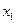
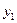
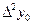
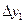
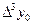
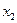
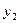
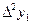
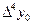
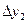
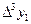
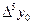
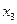
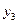
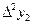
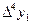
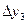
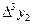
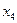
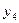
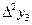
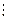
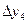
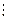
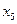
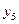
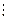
Будем строить интерполяционный многочлен следующим об­разом:

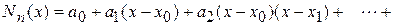
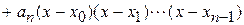. (7)

Коэффициенты 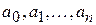будем определять из условия интерполяции 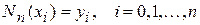, с использованием табли­цы (1):

;

;

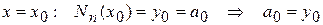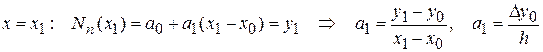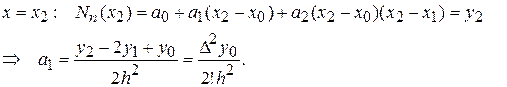
И так далее,

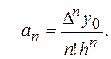
Подставляя коэффициенты 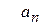в многочлен (7), полу­чим

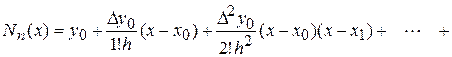
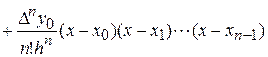. (8)

Многочлен (7) является интерполяционным многочленом, поскольку является многочленом n -й степени и удовлетворяет условию интерполяции (3). Он называется интерполяционным многочленом Ньютона или первым интерполяционным многочленом Ньютона. Его достоинство заключается в том, что он строится проще, чем 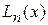, и при добавлении новых узлов интерполяции в таблицу (1) все предыдущие слагаемые не пересчитываются, а добавляются новые. К недостаткам многочле­на 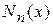по сравнению с 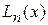, можно отнести использование постоянного шага между узлами интерполяции.

В силу единственности многочленной интерполяции очевидно, что

.

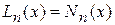Погрешность многочленной интерполяции.

Ясно, что в узлах интерполяции погрешность интерполяционно­го многочлена 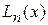или 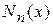равна нулю:

.

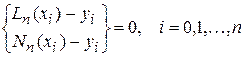Будем искать погрешность 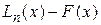в виде разности меж­ду значением интерполяционного многочлена 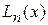и значением функции 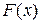в точке 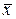, не совпадающей с узлом интерполяции.

Для нахождения погрешности составим следующую вспомо­гательную функцию:

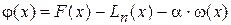, (9)

где 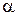подлежит определению, a 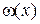— многочлен (п + 1)-й степени:

.

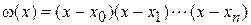Очевидно, что производные равны

, .

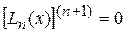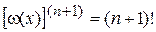Будем искать 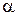из условия, что 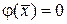в точке:

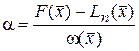. (10)

Функция 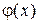имеет (п + 1) корень в узлах интерполяции, так как там 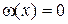и погрешность 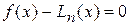. Но если добавим еще точку 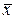, в которой потребуем 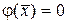, то 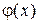будет иметь уже (п + 2) корня. Покажем, что увеличение порядка производной функции 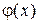на единицу уменьшает количество корней этой функции на единицу. Данное утверждение следует из теоремы Роля: если функция 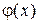на 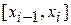непрерывна, дифференцируема на интервале 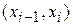и имеет на концах одинаковые значения, то внутри этого интервала найдется хотя бы одна точка, в которой производная этой функции равна нулю. Функция 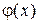на каждом отрезке удовлетворяет теореме Ролля (рис. 2).

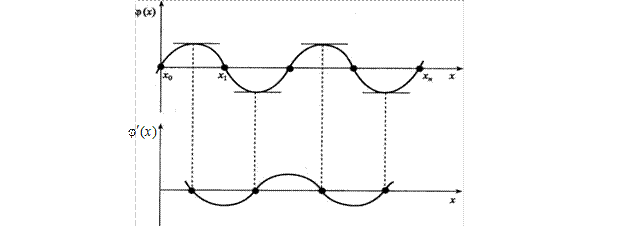Рис. 2 Соотношения количества нулей функци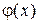й и .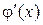

Итак 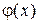имеет (п + 2) корня, 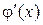имеет (п + 1) корень, 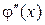имеет п корней и т.д., 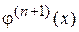имеет 1 корень. Обозначим этот корень через .

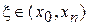Вычисляя производную (п+ 1)-го порядка от (9) в точке 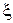и учитывая, что значение 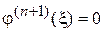, получим

,

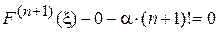откуда

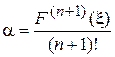. (11)

Подставляя (11) в (10), находим погрешность многочленной интерполяции в точке :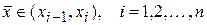

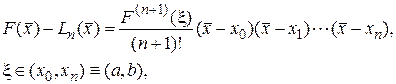(12)

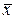– точка, в которой ищется погрешность, не совпадает с узлами интерполяции.

Поскольку точка 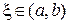неизвестна, то вместо погрешно­сти (12) вводится верхняя оценка погрешности в виде

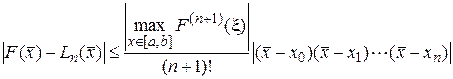, (13)

которая и используется на практике.

В случае если интерполяционный многочлен строится для экспериментальной таблицы (1), функция 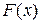отсутствует и погрешностью в форме (12) или (13) воспользоваться не удается. Тогда, в силу отмеченной связи между производными и конечными разностями, очень грубо можно заменить 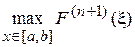на величину 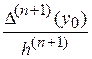, если, конечно, разности 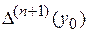еще несут какую-то информацию об 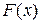, т.е. если степень п интерполяционного многочлена берется заниженной по сравнению с той, какой она должна быть для достижения максимальной точности при конкретном порядке практически постоянных разностей. В этом случае имеем оценку

.

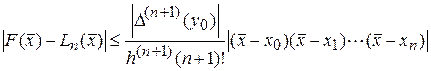Интерполяция многочленами реализует следующие идеи: исследуемая функция заменяется простой функцией – многочленом, критерием близости является совпадение интерполирующего многочлена и интерполируемой функции в заданных точках области определения. Однако интерполяция полиномом имеем ряд существенных недостатков. На практике для достижения разумной точности интерполяции приходиться прибегать к многочленам высоких степеней, что не всегда удобно.

Трудности, возникающие при многочленной интерполяции, хорошо иллюстрируются примером Рунге: интерполяция на от­резке [-1, 1] функции 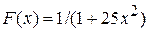при равномерном рас­пределении узлов. С увеличением порядка п интерполяционного многочлена возрастают колебательные свойства мно­гочлена, и это приводит к тому, что интерполяционный много­член расходится.

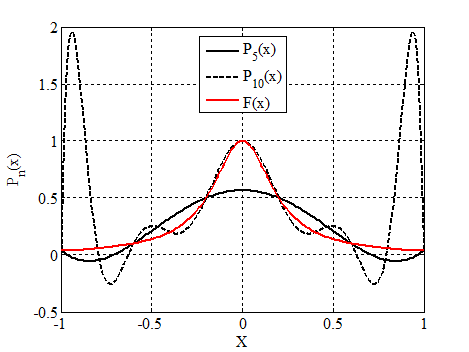
Рис. 3. Пример Рунге

Итак, многочленная аппроксимация, использующая сразу все узлы таблицы (глобальная интерполяция) имеет существенный недостаток – возможность появления больших экстремумов в промежутках между узлами сетки. Т.е. интерполяционный полином может иметь колебания, не свойственные исходным данным. Кроме того, с ростом степени полинома происходит быстрое накопление ошибок округления. Чтобы избежать этих нежелательных эффектов, на практике применяют кусочно-полиномиальную интерполяцию – многочленная интерполяция, осуществляемая по нескольким узлам таблицы (1) (локальная интерполяция).

Самой простой является кусочно-линейная интерполяция.

Пусть заданы значения 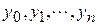некоторой функции , в узлах сетки :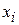

.

		……..		…….
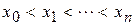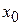
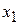
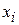
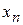
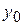
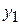
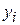
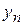
		………		……….		(1)

Требуется найти кусочно-линейную функцию 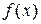такую, чтобы она приближала функцию 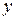, в том смысле, чтобы

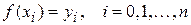. (2)

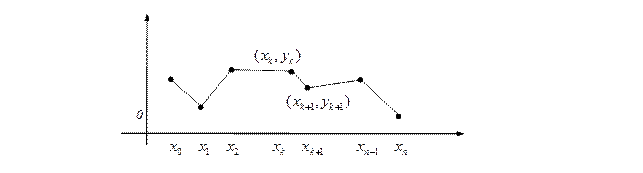
Рис. 4. Кусочно-линейная интерполяция

Решение задачи имеет вид

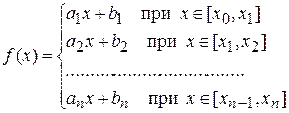. (3)

Для нахождения 2 n неизвестных коэффициентов 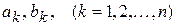имеем систему из 2 n линейных уравнений

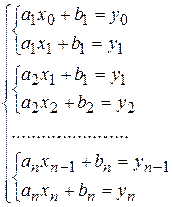, (4)

причем, каждая пара соседних уравнений системы, имеющих коэффициенты с одинаковыми индексами, не связана с остальными и может решаться отдельно. Таким образом, линейная интерполяция осуществляется по двум узлам, перемещаемым вдоль таблицы (1).

Однако такая интерполяция страдает тем недостатком, что интерполирующая функция в узлах стыковки многочлена теряет гладкость.

От этих недостатков свободна сплайн-интерполяция, которая требует непрерывности в узлах стыковки локальных многочленов по производным порядка один, два и т.д.

Пусть на отрезке 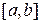заданная упорядоченная система несовпадающих точек .

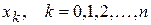Определение. Сплайном 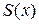называется определенная на 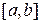функция, принадлежащая классу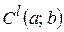 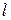раз непрерывно дифференцируемых функций, такая, что на каждом промежутку 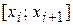, 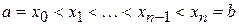– это многочлен степени - .

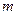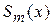Разность 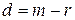между степенью сплайна 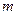и показателем её гладкости 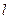называется дефектом сплайна.

Если сплайн 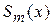строиться по некоторой сеточной функции 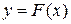так, чтобы выполнялись условия

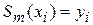, (где 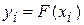- значения функции в узлах 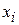сетки)

то такой сплайн называется интерполяционным сплайном для функции .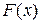

Например, кусочно-линейная функция 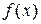, определенная в (1) с параметрами 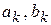, удовлетворяющими условиям (2) является сплайном 1- степени дефекта 1.

Однако совпадение дефекта сплайна с его степенью обеспечивает просто непрерывность сплайна. Интерес представляет построение сплайнов с большой гладкостью, т.е. с малым дефектом.

Наиболее распространенными являются сплайны 3-ей степени дефекта один, т.е. дважды (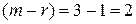) непрерывно дифференцируемый многочлен 3-ей степени на каждом отрезке 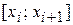, 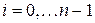. Сплайны, удовлетворяющие условию интерполяции, называются интерполяционными.

Наиболее известным и широко применяемым интерполяционным сплайном является сплайн степени 3 дефекта 1.

Определение. Кубическим сплайном дефекта 1, интерполирующим на отрезке 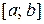данную сеточную функцию 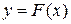, называется функция 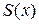, удовлетворяющая условиям

а) ,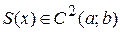

(т.е. непрерывна вместе со своими производными до второго порядка включительно);

б) на каждом из отрезков 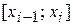функция 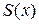является кубическим многочленом вида

,

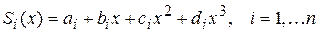где 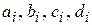– неизвестные коэффициенты сплайна;

в) в узлах сетки 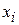выполняются равенства

.

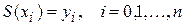Определение коэффициентов интерполяционного кубического сплайна.

Задача кусочно-кубической интерполяции ставится следующим образом. На отрезке 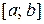необходимо найти функцию 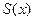, удовлетворяющую требованиям а), б), в) определения.

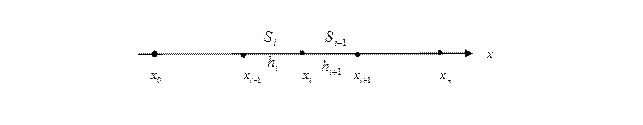Рис. 6. Узлы интерполяции

Из определения следует, что для построения кубического сплайна необходимо найти 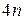коэффициентов 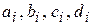. Рассмотрим как строятся уравнения.

В каждом внутреннем узле, согласно условиям непрерывности сплайна, должны выполняться равенства

,

,

,

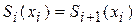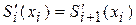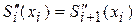Получим 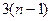уравнений.

Условия интерполяции дают еще 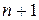уравнение:

, .

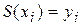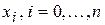Таким образом, всего 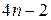уравнения для определения 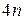неизвестных. Недостающие два уравнения получают из граничных условий. Граничные условия могут формулироваться по разному. Одни из них называются естественными краевыми условиями и выглядят так:

,

.

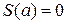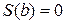С учетом краевых условий приходим к системе из 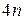линейных алгебраических уравнений относительно 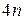неизвестных .

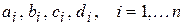Определенный таким образом сплайн называют естественным.

Замечание. Краевые условия в определении могут быть заменены на другие. Например, можно наложить дополнительные условия на первую производную функции 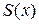в точках a и b. В таком случае кубический сплайн, оставаясь интерполяционным дефекта 1, утрачивает свойство быть естественным.

7.3. Метод наименьших квадратов.

Количественная характеристика отклонения двух функций.

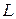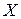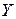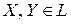Всякое множество элементов произвольной природы называется мет­рическим пространством, если для любых его элементов и () определено вещественное неотрицательное число, на­зываемое расстоянием 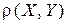между X и Y, удовлетворяющее следующим требованиям:

1) 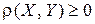, причем 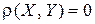тогда и только тогда, когда X = Y;

2) 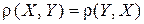- аксиома симметрии;

3) для любых трех элементов X, Y, Z 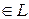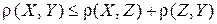- аксиома треугольника.

Примеры метрических пространств:

1. Множестве n -мерных векторов 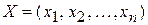– пространство 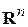. Расстояние между элементами определя­ется формулой

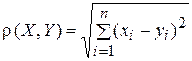. (1)

2. Пространство функций 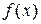, непрерывных на интервале – .

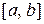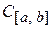Расстояние между элементам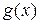и и 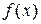, 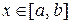этого пространства определяется как

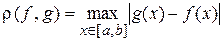, (2)

т.е. как максимальное расстояние между кривыми (рис.6.7) на отрезке.

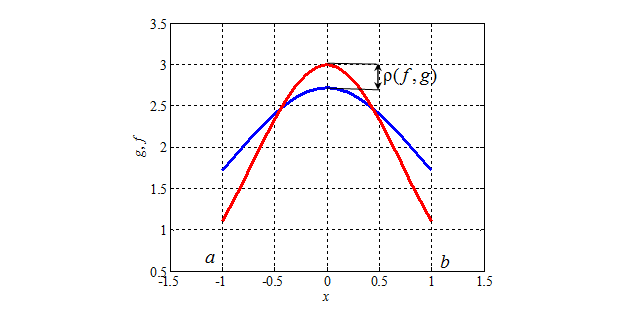Рис.6.7. Расстояние между функциями в пространстве С

3. Пространство функций , определенных на интервале и таких что

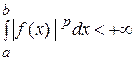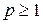, (3)

Обозначение – 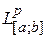. Такие функции называют суммируемыми с р- ой степенью. При этом вводят следующее расстояние между элементами пространства

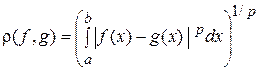. (4)

В частности, при р = 2

.

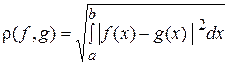Можно показать, что расстояния (1) - (4) удовлетворяют всем аксиомам метрического пространства.

Так в теории аппроксимации метрика того или иного пространства принимается за меру отклонения аппроксимирующей функции 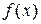и заданной 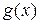. При этом для заданной точности 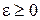условие

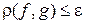, (5)

может иметь существенное качественное различие в зависимости от вида используемого метрического пространства. Действительно, для пространства С условие (5) ограничивает выход аппроксими­рующей функции 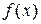за пределы интервала 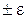от ординат 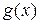(рис. 8). В этом случае говорят о равномерном приближении функции .

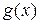Рис. 8	Рис. 9

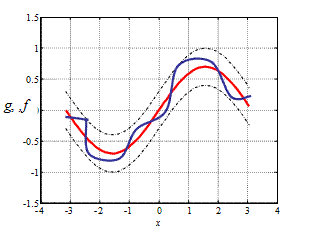
Для пространства 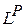условие (5) допускает значительное от­клонение от функци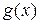й и 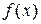на малых интервалах изменения 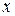(рис. 9). При этом говорят о приближении в среднем. В частности при р = 2 говорят о среднеквадратичном приближении.

Характер опытных данных. Задача аппроксимации.

Пусть результаты некоторого опыта или наблюдений представлены в виде таблицы. Такую таблицу будем называть экспериментальной таблицей.

		………………..
		………………..

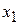
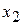
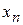
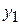
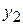
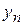
Ранее при интерполировании табличной функций мы использовали условие равенства значений интерполирующей функции и заданной функции в узлах таблицы

.

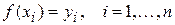Соблюдение этого требования имеет смысл, если опытные данные считать точными. Однако на практике при обработке результатов эксперимента возникают ошибки данных по разным причинам (субъективные причины, несовершенство измерительного прибора и т.д.). Эти ошибки делят на три категории: систематические, случайные и грубые.

Систематические ошибки обычно дают отклонение в одну сторону от истинного значения измеряемой величины. Они могут быть постоянными или закономерно изменяться при повторении опыта, и их причина и характер известны. Например, они могут быть вызваны условиями эксперимента (влажностью, температурой среды и т.д.), дефектом измерительного прибора. Эти ошибки могут быть учтены введением соответствующих поправок.

Случайные ошибки определяются большим числом факторов, которые не могут быть учтены при измерениях или при обработке результатов. Они имеют случайный (несистематический характер) и дают отклонения от средней величины в ту и другую сторону и не могут быть устранены в эксперименте. Статистическая обработка данных позволяет определить величину случайной ошибки и довести её до некоторого приемлемого значения повторением измерений достаточное число раз.

Грубые ошибки явно искажают результат измерения, они чрезмерно большие и обычно пропадают при повторении опыта. Грубые ошибки существенно выходят за пределы случайной ошибки, полученной при статистической обработке. Измерения с такими ошибками отбрасываются и в расчет при окончательной обработке результатов измерений не принимаются.

Таким образом, в опытных данных всегда имеется случайная ошибка.

Ставится задача отыскания приближенной функции 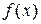для функции, заданной в виде экспериментальной таблицы, такой, чтобы величина отклонения (определенного в некотором смысле) этих функций является минимальной, т.е. решать задачу аппроксимации.

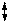
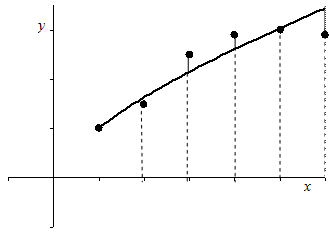
Рис. 6.10. Отклонение аппроксимирующей функции от табличной

Значения 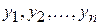табличной функции мы можем рассматривать как координаты некоторого вектора 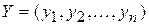в п - мер­ном пространстве 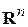. Аналогично и для значений функ­ции 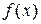: 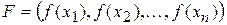. Тем самым в соответ­ствии с представлением метрики в пространстве 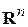расстояние между векторам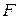и и 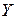или, что то же самое, между функциям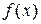и и на точечном множестве 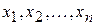, может быть определено с помощью формулы

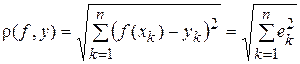, (6)

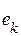– отклонения в узлах таблицы

Если, в качестве критерия аппроксимации принять требование

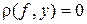, (7)

то будем иметь частный случай аппроксимации - интерполяцию. Однако, очевидно, что далеко не всякая функция 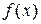может обе­спечить выполнение условия (7).

Представим аппроксимирующую функцию в виде

,

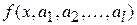где 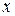– независимая переменная, 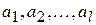– набор неизвестных постоянных параметров и поставим задачу нахождения таких значений параметров 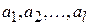, при которых функция расстояния (6) имеет минимум

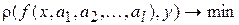. (8)

Таким образом, условие (8) и будет выступать в качестве критерия аппроксимации.

Однако на практике ищут минимум не функции (8), а её квадрата,

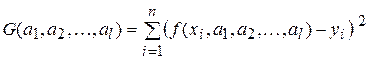, (9)

функции, которая представляет собой сумму квадратов отклонений .

Процедура определения параметров из условия минимума функции (9) называется методом наименьших квадратов.

Линейная аппроксимация.

Одной из наиболее часто используемых в методе наименьших квадратов функций является прямая, описываемая уравнением вида

.

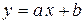Параметры a и b –называются коэффициентами линейной регрессии.

Согласно методу наименьших квадратов, коэффициенты a и b подберем так, чтобы функция двух переменных

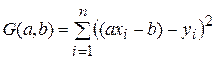
получила минимальное значение.

Для этого необходимо, чтобы

.

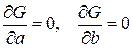В результате дифференцирования, получаем систему линейных алгебраических уравнений в виде

.

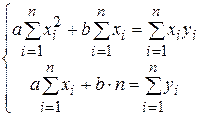Из решения этой системы найдем a и b и подставим в уравнение искомой прямой.

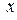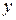Показатель, характеризующий тесноту линейной связи между и называется коэффициентом корреляции и рассчитывается по формуле

,

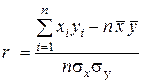где

, ,

, , ,

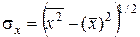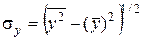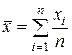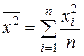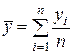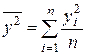
Значение коэффициента корреляции удовлетворяет соотношению

.

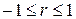Чем меньше отличается абсолютная величина 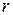от единицы, тем ближе к линии регрессии располагаются экспериментальные точки. Если коэффициент корреляции близок к нулю, то это означает, что между 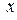и 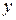отсутствует линейная связь, но может существовать другая нелинейная зависимость. Чтобы проверить, значительно ли отличается от нуля коэффициент корреляции, используют критерий Стьюдента. Значение критерия вычисляется по формуле

.

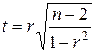Вычисленное значение 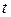сравнивается со значением, взятым из таблицы распределения Стьюдента, в соответствии с уровнем значимости 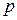и числом степеней свободы 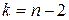. Если 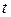больше табличного, то коэффициент корреляции значительно отличен от нуля.

Метод выравнивания.

Рассмотрим частный случай. Пусть из некоторых соображений для аппроксимации табличных данных используется степенная функция:

,

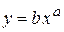где a и b – свободные параметры, причем 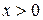и 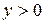. Логарифмируем равенство :

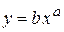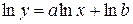
и вводим обозначения , , .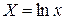

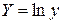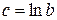Тогда получим линейную связь между новыми переменными

,

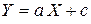коэффициенты которой находим из решения системы

,

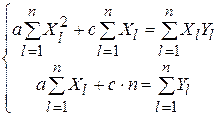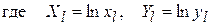
Тогда, искомая функциональная зависимость будет иметь вид

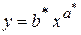, где .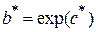

Прием, который использовался в данной задаче и состоял в преобразовании исходного соотношения к линейному уравнению, лежит в основе метода выравнивания.

Укажем ещё несколько соотношений с двумя параметрами, которые легко преобразуются к линейному уравнению :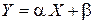

;

;

;

;

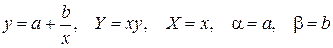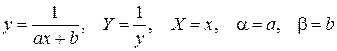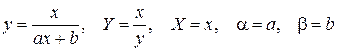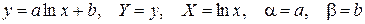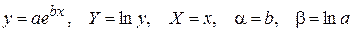
Аппроксимация квадратичной функцией.

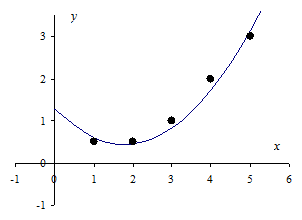
Пример. Дана таблица значений функции:

x
y	0,5	0,5

Определить вид зависимости между величинами x и y.

Решение. В прямоугольной декартовой системе координат построим точки 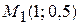, , 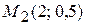, , 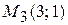, , 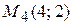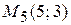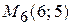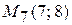. Предположим, что точки незначительно уклоняются от дуги некоторой параболы. Следовательно, зависимость между x и y выражается формулой

,

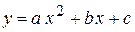где a, b и c – неизвестные коэффициенты, подлежащие определению. Параметры a, b, c выберем так, чтобы функция трех переменных

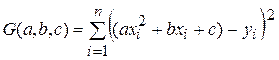
была минимальной. Для этого необходимо, чтобы

.

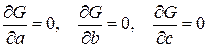В результате получаем нормальную систему:

.

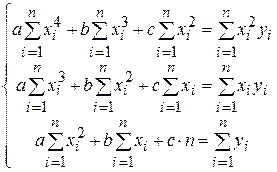Для данной таблицы 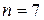система нормальных уравнений имеет вид

.

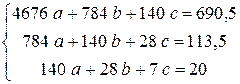Решение системы: .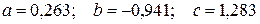

Искомый многочлен имеет вид – .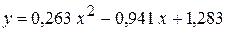

Дата добавления: 2014-01-07