Особые точки и вид ряда Лорана

Точка а называется изолированной особой точкой функции f(z), если найдется окрестность точки а, в которой функция f(z) аналитична и аналитичность нарушается при переходе к самой точке.

Более точное определение:

Точка а называется изолированной особой точкой функции f(z), если найдется кольцо К, вида 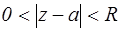, в котором функция f(z) аналитична и аналитичность не имеет места в самой точке.

Различают три типа изолированных особых точек:

1. изолированная особая точка а называется устранимой, если существует .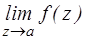

Пример.

z=0 – устранимая изолированная особая точка функции 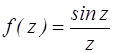, т. к.

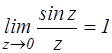
Название устранимая особая точка оправдывается тем, что особенность функции в этой точке можно устранить, если положить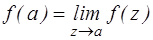

2. изолированная особая точка а называется полюсом, если функция f(z) неограниченно возрастает при .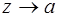

Пример.

z=3 – полюс точка функции .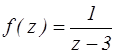

Каждый полюс а функции f(z) является нулем а функции .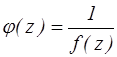

Порядком полюса а функции f(z) называют порядок нуля а функции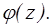

Говорят, что точка а является нулем функции 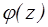порядка m, если .

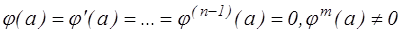Пример.

z=3 – полюс третьего порядка функции .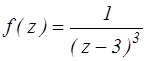

3. изолированная особая точка а называется существенно особой, если не существует .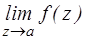

Пример.

z=0 - существенно особая точка функции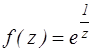

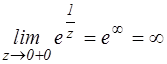
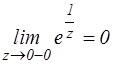
рис. 1

По определению изолированной особой точки существует кольцо

К: 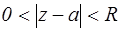, в котором функция f(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана:

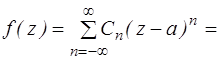
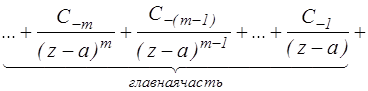
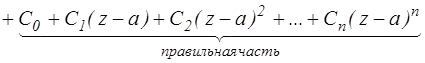
Сумма членов ряда Лорана, содержащих отрицательные степени 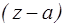называются главной частью ряда Лорана. Сумма членов ряда Лорана, содержащих положительные степени называется правильной частью ряда Лорана.

Могут иметь место три случая:

1) ряд Лорана содержит только правильную часть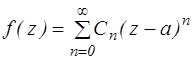

Тогда 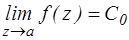, т. е. точка а –устранимая особая точка.

2) ряд Лорана содержит конечную главную часть

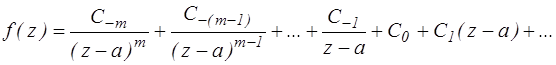
Представим:

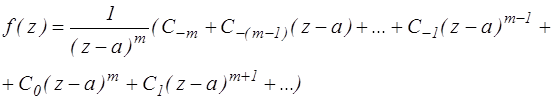
Можно видеть, что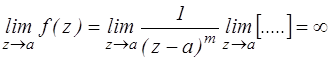

Точка а – является полюсом функции f(z). В ТФКП, доказывается, что порядок полюса совпадает с числом членов в главной части ряда Лорана.

3) ряд Лорана содержит бесконечную главную часть

В ТФКП, доказывается, что точка а– является существенно особой точкой функции f(z).

Пусть точка а –изолированная особая точка функции f(z). По определению существует кольцо К: 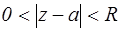, в котором функция f(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана по степеням 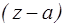. В этом разложении особую роль играет коэффициент 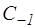,(коэффициент при сомножителе 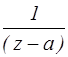), который называется вычетом функции f(z) в точке z=a и обозначается 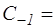Res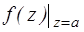

Дата добавления: 2014-01-14