Внезапное расширение. Теорема Борда (Борда – Карно)

Внезапное расширение показано на рис.7-4, 1-1 - входное сечение, 2-2 – выходное.

Пусть как во входном, так и в выходном сечениях поток однородный, скорость поперек сечения постоянна, . Вычислим .

Траектория частиц жидкости, проходящих поворот, не может иметь излом, так как это означало бы, что радиус кривизны →0, а нулевой радиус кривизны означает бесконечно большую центробежную силу. Таким образом, траектория частицы может меняться только плавно. При этом в углах за расширением образуются водовороты, течение в них существенно турбулентное. Нарушение однородной структуры течения в углах является причиной потерь давления на внезапном расширении.

Пусть известны диаметры трубы до и после расширения и параметры потока во входном сечении: скорость 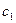и давление 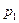, а также плотность 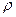, которую будем считать постоянной.

Запишем уравнение неразрывности (при стационарном течении несжимаемой жидкости сохраняется объемный расход):

(1)

и уравнение Бернулли (интеграл Бернулли) для несжимаемой жидкости:

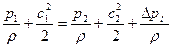(2)

В последнем слагаемом справа в (2) потери механической энергии выражены через потери давления на местном сопротивлении.

Скорость может быть выражена из первого уравнения, но во втором два неизвестных: 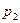и .

Следовательно, нужно искать третье уравнение, причем задача представляет собой «черный ящик»: мы хотим узнать, что делается на выходе (в сечении 2-2), не имея ясного представления о том, что происходит внутри (непосредственно на внезапном расширении).

Мы использовали закон сохранения массы - уравнение неразрывности, закон сохранения энергии – в форме уравнения Бернулли. Из основных законов сохранения остался незадействованным закон сохранения количества движения. Закон этот утверждает, что внутренние силы не меняют количество движения; изменение количества движения равно главному вектору внешних сил, что нас как раз устраивает, поскольку внутренних сил (то, что происходит на самом внезапном расширении) мы не знаем.

Поэтому сделаем лирическое отступление и выведем закон сохранения количества движения.

Дата добавления: 2014-01-14