Интегральное преобразование Фурье

Интегральные преобразования тесно связаны с рядами Фурье. До сих пор с любой кусочно-непрерывной функцией мы связывали ряд Фурье. Иногда имеет смысл заменить ряд несобственным интегралом. Покажем, как это можно сделать на примере тригонометрического ряда Фурье в комплексной форме.

Мы знаем, что любой кусочно-непрерывной на отрезке 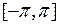функции 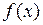можно поставить в соответствие ряд Фурье 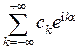, где

, .

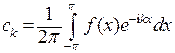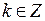Представим теперь, что 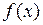кусочно-непрерывна на отрезке 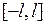. Путем простейшей замены 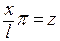мы преобразуем отрезок 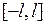в отрезок 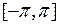и для функции 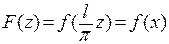построим соответствующий ряд, выраженный через переменную 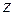. Возвращаясь к старой переменной, получим 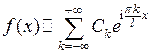, где

.

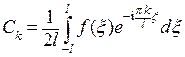Предположим теперь, что 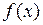кусочно-непрерывна на отрезке 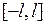при любом 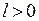и существует несобственный интеграл 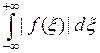. Обозначим 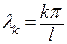и 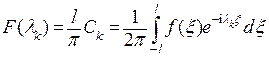. Очевидно, что 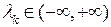. Тогда

.

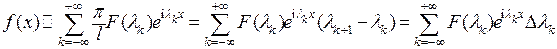Последнее выражение в цепочке равенств – это интегральная сумма функции 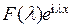. Пусть 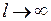, тогда 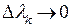, и интегральная сумма превращается в интеграл. Тогда в точках непрерывности 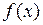мы получим представление

,

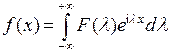где

.

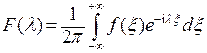Запишем последние две формулы в несколько ином виде:

,

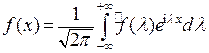где

.

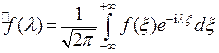Представление функции 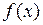с помощью интеграла от функции 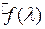называется представлением функции в виде интеграла Фурье, а выражение функции 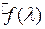с помощью 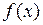называется интегральным преобразованием Фурье. Первое представление еще называют и обратным преобразованием Фурье.

Заметим, что интегральное преобразование Фурье удобно использовать в дифференциальных уравнениях, так как 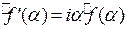. Докажем это, пользуясь тем, что существование 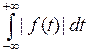предполагает, что .

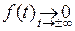Действительно, используя формулу интегрирования по частям, получим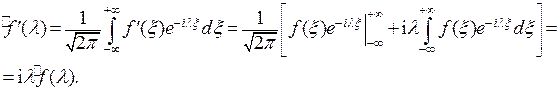

П р и м е р. Найти решение 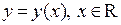, дифференциального уравнения 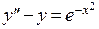, которое удовлетворяет условию: .

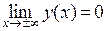Заметим, что условие на поведение решения в окрестности бесконечно удаленной точки является заменой начальным или краевым условиям. Кроме того, это условие мешает применить, например, степенные ряды для получения решения, несмотря на то, что само уравнение является линейным. Поэтому применим интегральное преобразование Фурье. Для этого обе части уравнения 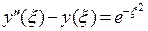умножим на 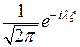и проинтегрируем по 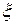на бесконечном интервале 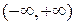. Согласно введенному обозначению и свойству преобразования Фурье от производной получим 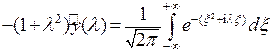. Следовательно,

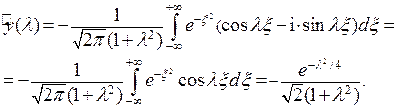
Теперь для того, чтобы получить решение, достаточно вернуться от интегрального преобразования к самой функции 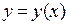с помощью интеграла Фурье: .

То, что найденное решение удовлетворяет заданным условиям вблизи бесконечно удаленной точки, легко проверить с помощью интегрирования по частям.

Дата добавления: 2014-01-14