Й учебный вопрос. Понятие о регрессионном анализе

С помощью регрессионного анализа устанавливается аналитический вид взаимосвязи:

- между двумя факторами (парный анализ);

- между совокупностью факторов (множественный анализ)

Установление аналитического вида взаимосвязи при использовании парного и множественного регрессионного анализа сводится к следующему. Во-первых, задается вид функции, во-вторых, определяется неизвестные значения параметров этой функции. При решении последней из указанных выше задач используется метод наименьших квадратов.

Предположим, что для функции известны значения на некотором конечном множестве точек 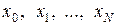(пусть 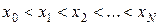), причем в узловых точках 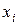, , 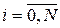функция задана с погрешностью. Требуется по исходной информации наилучшим образом восстановить функцию .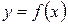

Определение. Среднеквадратичная аппроксимация – это нахождение для заданной функции другой функции 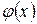из некоторого класса функций, для которой среднеквадратичное отклонение (сумма квадратов отклонения функции в узлах интерполирования) от заданной функции минимально.

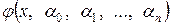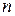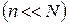Функцию, с помощью которой решают задачу аппроксимации, иногда называют аппроксимантом. Пусть – аппроксимант, где – варьируемые параметры, – максимальный показатель степени, а – число узловых точек , тогда можно дать формальное описание задачи аппроксимации функции :

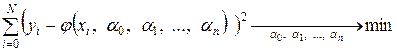. (3.17)

Рассматриваемую задачу можно интерпретировать как проведение аппроксимирующей функции 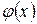между узлами аппроксимации исходной функции так, чтобы сумма квадратов отклонений 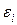функции 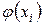от точек 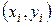, , 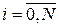была наименьшей (рис. 3.2).

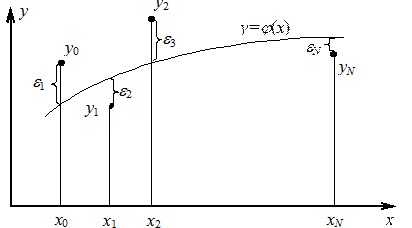
Рис. 3.2. Задача аппроксимации функции .

Практической реализацией среднеквадратичной аппроксимации является метод наименьших квадратов. Нахождение параметров связи между аргументом и значением функции, абстрагируясь от случайностей, является задачей регрессионного анализа, при этом получают теоретическую линию регрессии. Теоретической линией регрессии (трендом) называется линия, вокруг которой группируются значения переменных и которая указывает основное направление или основную тенденцию связи.

Регрессионный анализ – это статистический метод исследования зависимости между зависимой переменной и одной или несколькими независимыми переменными. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные – критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения. Одной из основных целей регрессионного анализа является определение наличия математического уравнения связи между переменными.

В общем случае, задачей регрессионного анализа является определение вида и параметров зависимости 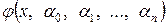, при этом вид зависимости, как правило, определяется экспертом на основании эмпирических данных. Выбранная функция должна проходить как можно ближе к значениям, которые были получены экспериментально при статистическом наблюдении. Если функция проходит через все экспериментальные значения, то она принимает на себя все ошибки, и это может быть достигнуто только в том случае, когда в регрессионной модели были учтены факторы (в том числе достоверно неизвестные), которые оказывают небольшое или косвенное воздействие. В связи с этим, отбросив ряд факторов, использовать в регрессионном анализе многочлен высокой степени нецелесообразно.

Основная особенность задачи аппроксимации функции заключается в том, что точные измерения значений 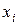, а также , , 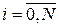представляются невозможными, то есть связанными с различного рода ошибками и погрешностями. Поэтому, чтобы исключить влияние ошибок, каждая из которых не имеет решающего влияния на результаты измерений (не подавляет остальные ошибки), производится большое число измерений, каждое из которых по сути дает уравнение, связывающее неизвестные коэффициенты со значениями и 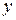. Следовательно, формируется система, число уравнений в которой значительно больше числа неизвестных. В результате, исходная задача сводится к отысканию наиболее вероятных значений коэффициентов , которые, вообще говоря, не будут точно удовлетворять ни одному из уравнений системы. Сформулируем представленные рассуждения в более общем виде. Пусть дана функция

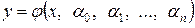(3.18)

независимой переменной и постоянных, но заранее неизвестных параметров 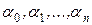. Для их выявления производится ряд измерений величин и 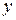, результаты которых преобразуют уравнение (3.18) в набор уравнений

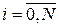, , (3.19)

где 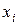и 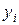– пары измеренных значений, а – число измерений.

Если бы значения и 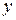измерялись точно, то для отыскания параметров достаточно было бы провести измерений. Но так как на самом деле значения и 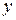содержат ошибки, никакие измерений не позволят определить истинные значения параметров . Поэтому обычно производится большое число измерений , в результате чего число уравнений (3.19) будет существенно больше числа неизвестных параметров. В этом случае система уравнений (3.19) будет, вообще говоря, несовместной, то есть точные решения каких-либо уравнений системы могут не удовлетворять остальным уравнениям.

В результате исходная задача сводится к отысканию таких значений неизвестных параметров , которые будут удовлетворять всем уравнениям наилучшим образом. Другими словами, требуется найти наиболее вероятные значения неизвестных параметров, которые будут тем более близки к истинным, чем больше измерений было сделано.

Так как уравнения (3.19) удовлетворяются неточно, то

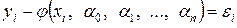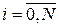, , (3.20)

где 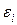– отклонения измеренных значений 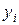от вычисленных по формуле (3.18).

Принцип минимизации отклонений, положенный в основу метода наименьших квадратов, утверждает, что наивероятнейшими значениями параметров будут такие, при которых сумма квадратов отклонений будет наименьшей, то есть реализуется формальное описание задачи (3.17). При этом считается, что отклонения 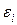подчиняются нормальному закону распределения в силу указанной выше особенности ошибок, когда все они имеют одинаковое влияние и ни одна из них не подавляет другие.

Рассматривая в (3.17) параметры как независимые переменные и приравнивая к нулю частные производные от левой части по этим переменным, получим уравнение с неизвестными. В результате требуется найти решение системы нормальных уравнений Гаусса: , где 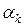– неизвестный параметр, .

Решение указанной системы уравнений (3.20) будет содержать такие значения параметров , при которых сумма квадратов отклонений 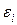, , 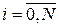минимальна:

.

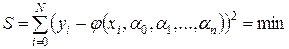Системы нормальных уравнений, позволяющие определять параметры некоторых регрессионных моделей, представлены в табл. 3.2, где по знаком 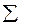понимается суммирование по 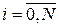, а соответствующий индекс в суммируемых величинах не указывается.

Дата добавления: 2014-01-14