Й учебный вопрос. Парная линейная регрессия.

Обратимся к парному регрессионному анализу, когда устанавливается аналитический вид взаимосвязи между двумя факторами X и Y. Исходными данными в данном случае является N совокупность пар значений X_n и Y_n, поставленных в соответствии друг другу.

Предположим, что в качестве заданной функции, определяющей взаимосвязь независимой и зависимой переменной X и Y, используется функция 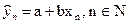, где a и b неизвестные значения параметров этой функции, 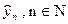- значения оценки зависимой переменной, соответствующей лини регрессии, определяемой заданной функцией.

Целевая функция метода наименьших квадратов для заданной функции 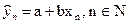, имеет вид (81)

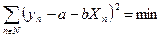
(81)

Эта функция зависит от неизвестных значений параметров a и b. Таким образом, может быть введено соотношение (82)

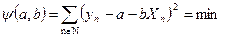
(82)

Для того, чтобы найти значения параметров a и b, обращающих функцию 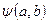в минимум, необходимо следующее:

1. продифференцировать функцию 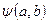по переменным a и b;

2. полученные выражения приравнять нулю;

3. решить систему полученных уравнений;

В результате будем иметь следующие соотношения

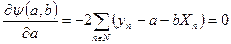
	(83)
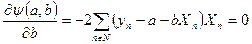
	(84)

Умножим левую и правую часть выражений (83) и (84) на -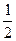. В результате получим

	(85)
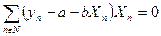
	(86)

Преобразуем соотношения (85) и (86). В результате получим

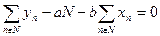
	(87)
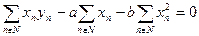
	(88)

Умножим левую и правую часть выражений (87) и (88) на 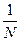. В итоге получим

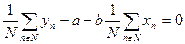
	(89)
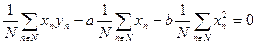
	(90)

Являются справедливыми соотношения (91) – (94)

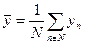
	(91)
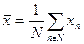
	(92)
	(93)
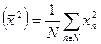
	(94)

В этом случае выражения (89) и (90) преобразуются к виду (95) и (96)

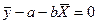
	(95)
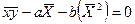
	(96)

Выразим a из соотношения (95) через y, 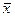и b. В результате получим

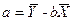
(97)

Подставим выражение (97) в соотношение (96). В итоге получим

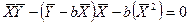
(98)

Преобразуем соотношение (98), в результате чего получим

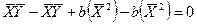
(99)

Отсюда может быть найдено выражение (100), с помощью которого определяется неизвестное значение параметра b

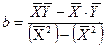
(100)

Подставляя значение b в формулу (97), находим неизвестное значение параметра a.

Найдем связь между параметром b, значение которого рассчитывается по формуле (100) и коэффициентом линейной парной корреляции, значение которого рассчитывается по формуле (101)

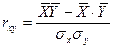
(101)

Для этого возьмем формулу (102), с помощью которой определяется дисперсия независимой переменной X

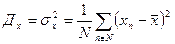
(102)

Преобразуем выражение (102). В итоге получим

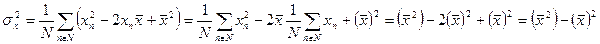
(103)

Подставляя выражение (103) в формулу (100), получаем

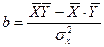
(104)

Разделим левую и правую часть выражения (104) соответственно на левую и правую часть выражения (101). В итоге получим

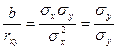
(105)

Таким образом, значение параметра b и коэффициента линейной парной корреляции r_xy связаны между собой с помощью соотношений (106) и (107)

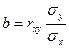
	(106)
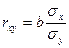
	(107)

Теорема Гаусса-Маркова доказывает следующие свойства метода наименьших квадратов. К ним относятся:

- несмещенность оценки, что означает, что математическое ожидание остатков 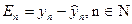, равно нулю; ;

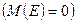- оценки являются эффективными; это значит, что дисперсия 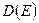является минимальной из возможных;

- оценки являются состоятельными; состоятельность оценки характеризуют увеличение ее точности с увеличением объема выборки;

- значения остатков 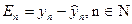, являются некоррелированы.

- остатки 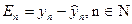,подчиняются нормальному закону распределения.

В итоге после использования метода наименьших квадратов и получения остатков необходима проверка следующих 5 предпосылок метода наименьших квадратов:

1. случайный характер остатков;

2. нулевая средняя величина остатков;

3. наличие гомоскедастичности, которая заключается в том, что дисперсия каждого отклонения E_n одинакова для всех значений Х;

4. отсутствие автокорреляции остатков;

5. предположения, что остатки подчиняются нормальному закону распределения.

Помимо линейной функции при использовании парного регрессионного анализа могут использоваться и другие функции.

Например, параболическая функция	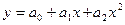(108)
Парная гиперболическая функция	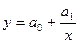(109)
Парная степенная функция	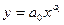(110)
Парная показательная функция	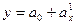(111)

С помощью метода наименьших квадратов могут быть найдены неизвестные значения параметров этих функций. При этом степенная и показательная функция должны быть предварительно приведены к линейному виду с помощью операции логарифмирования. В результате вместо соотношений (110) и (111) получаем

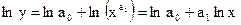
(110)

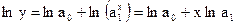
(111)

Для выбора наиболее предпочтительной функции из их некоторой заданной совокупности следует использовать следующий подход. В соответствии с ним для каждой отдельной функции с оцененными значениями параметров находится сумма квадратов отношений значений зависимой переменной Y от значения 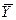, соответствующей линии регрессии, используя формулу (112)

(112)

Та функция, которой соответствует минимальное значение показателя и, является наиболее предпочтительней.

Дата добавления: 2014-01-14