Некоторые регрессионные модели

№	Вид модели	Уравнение модели	Система нормальных уравнений Гаусса
1.	Линейная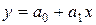
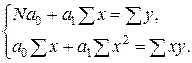
2.	Параболическая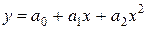
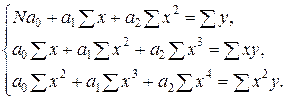
3.	Кубическая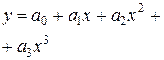
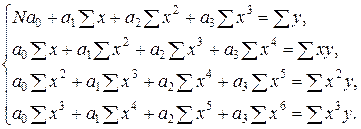
4.	Гиперболическая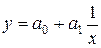
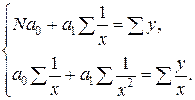
5.	Показательная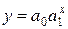
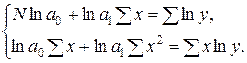
6.	Степенная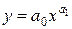
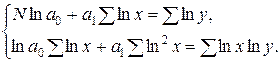
7.	Логарифмическая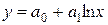

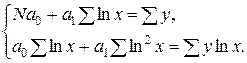
Проверка статистической значимости уравнения нелинейной регрессии в целом осуществляется через F -критерий Фишера и индекс детерминации R².

Индекс детерминации используется для проверки статистической значимости в целом уравнения нелинейной регрессии по F-критерию Фишера.

,

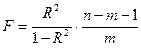где n – число наблюдений; m - число параметров при переменных х.

Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n-m-1) – число степеней свободы для остаточной суммы квадратов.

Так для степенной функции вида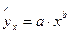 значение m =1 и формула принимает вид, что и при линейной зависимости: .

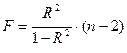Для параболы второй степени 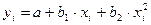число степеней свободы m =2. Отсюда: .

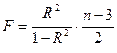Средняя ошибка аппроксимации – это среднее отклонение расчетных значений результативного признака от фактических: .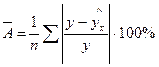

Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.

Различают 2 класса нелинейной регрессии (НР):

1. Регрессии нелинейные относительно включенных в анализ объясняющих переменных, но линейная по оцениваемым параметрам

2. Регрессии нелинейные по оцениваемым параметрам.

Пример: нелинейная регрессия по включенным в нее объясняющим переменным могут служить следующие функции: полиномы различных степеней, равносторонняя гипербола.

К НР по оцениваемым параметрам относительно следующей модели:

v Степенная у=ax×b×ε

v Показательная у=a×b^x × ε

v Экспотенциальная у= e^a+bx × ε

НР по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии - методом наименьших квадратов (МНК) так как эти функции линейны по параметрам. Так в параболе второй степени у=а₀ +а₁х +а₂х + ε, заменяя х=х₁,а x² =х₂ , получаем, двухфакторное уравнение регрессии: у₀=а₀ +а₁х₁ +а₂х₂ + ε для оценки параметров, которые, как известно, использует МНК.

Аналогично и для полинома К-порядка у=а₀ +а₁х +а₂х² + а₃х³+ …. + а_nхⁿ, получим линейную модель множества регрессии с К объясняющими переменными:

у=а₀ +а₁х₁ +а₂х₂ +……+ а_кх_к

Следовательно, полином любого порядка сводится к K - линейной регрессии, с ее методами оценивая параметров и проверки гипотез.

Как показывает опыт большинства исследователей среди нелинейной полиномной регрессии чаще всего используется парабола второй степени в отдельных случаях - полином третьего порядка.

Ограничения в использовании полиномов более высоких степеней связаны с требованиями однородности и исследования совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая, и тем менее однородна совокупность по признаку (результирующему).

Парабола второй степени целесообразна к применению, если для определенного интервала значение фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную, или обратная на прямую. В этом случае, определяется значение фактора, при котором достигается максимум (или минимум) значения результативного признака. Приравнивая к нулю первую производную параболы второй степени

ŷ_х= a+bx+cx²

ŷ′_х= b+2cx=0

x= -b/2c

Если исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становится трудно интегрируемы, а форма связи часто заменяется другими нелинейными моделями (НМ).

Применение МНК для оценки параметров параболы второго порядка приводит к следующим системам нормальных уравнений:

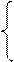∑у = na + b∑x +c ∑x²;

∑yx =a∑x +b∑ x² +c ∑x³;

∑yx²= a∑ x²+ b∑ x³+c ∑ x⁴;

Решение ее возможно методом определителей

a= ∆a/∆; b= ∆b/∆; c= ∆c/∆,

где ∆- определитель системы,

∆a, ∆b, ∆c – частные определители системы

При b>0 и c<0 кривая симметрична относительно своей высшей точки, то есть точки перелома кривой, изменений направление связи, а именно роста на ладони. Такого рода функцию можно наблюдать в экономике труда, при изучении зависимости зарплаты работников физического труда от возраста- с увеличением возраста повышается зарплата в связи с одновременным повышением опыта и увеличением квалификации работника. Однако, с определенного возраста, в виду старения и снижения производительности труда дальнейшее повышение возраста может приводить к снижению зарплаты. Если параболическая форма связи демонстрирует окончательный рост, а затем снижение уровня значения результативного признака, то определяется значение фактора, при котором достигается максимум. Так, предполагается, что потребление товара а (единиц) в зависимости от уровня дохода семьи характеризуется уравнением вида: ŷ_х = 5+6х-х² приравниваем к нулю первую производную найдем величину дохода, при котором потребление максимума велико.

При b<0 и c>0,парабола второго порядка симметрична относительно своей низшей точки, что позволяет определить минимум функции в точки, имеющей направление связи, т.е снижение на рост.

Так, если в зависимости от объема выпуска продукции, затраты на производство характеризуется при х=15

В виду симметричности кривой, парабола второй степени далеко не всегда пригодна в конкретном исследовании. Чаще, исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной парабольной формой. Кроме того, параметры парабольной связи не всегда могут быть логически интегрированы.

Поэтому, если график зависимости не демонстрирует четко выраженные параболы второго порядка (нет смены направленности связей-признаков), то она может быть заменена другой нелинейной функцией, например степенной.

В частности, в литературе, часто рассматривается парабола второй степени для характеристики зависимости урожайности от количества внесенных удобрений.

Данная форма связи мотивируется, что с количеством внесенных удобрений урожайность растет лишь до оптимальной дозы вносимых удобрений. Дальнейший же рост их дозы оказывается вредным для растений и урожайность снижается. На несомненную справедливость данного утверждения следует отметить, что внесение в почву минерального удобрения производится на основе учета достижений аэробиологической науки.

Поэтому, на практике, часто данная зависимость представлена лишь сегментом параболы, что и позволяет использовать другие нелинейные функции.

В качестве примера рассмотрим следующую зависимость:

Внесено минерального удобрения ц. на 1 га	Урожайность ц. на 1 га
Х	У

В соответствии с данными значениями система нормальных уравнений составят:

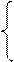5a+15b+55c=50

15a+55b+225c=167

55a+225b+979c=648

Решая ее методом определителей, получим:

∆ =700, ∆а=2380, ∆b=2090, ∆c= -150

откуда параметры искомого уравнения составят:

a=3.4

b=2.986

c= -0.214,

а уравнения параболы второй степени примет вид: ŷ_х=3,4 +2,986х – 0,214 х²

Подставляя в это уравнение последовательно значения Х, найдем теоретические (модельные) значения ŷ_х Уравнение параболы второго порядка достаточно хорошо описывает рассматриваемую зависимость. Сумма квадратов отклонений остаточных величин: ∑(у- ŷ_х)²=0,46

В виду того, что данные демонстрируют лишь сегмент параболы второго порядка, то рассматриваемая зависимость может быть охарактеризована и другой функцией, используя, в частности, степенную функцию: ŷ_х =ax^b было получено уравнение регрессии: ŷ_х = 6,136 х^0,474.Для чего: ∑(у- ŷ_х)²=0,43,Что означает еще лучшую сходимость фактических и расчетных значений у.

Среди класса нелинейных моделей, параметры, которые без особых затруднений оцениваются МНК, следует хорошо известную в эконометрике равностороннюю гиперболу: ŷ_х=а+(b/x).

Она может быть использована для характеристики связей удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции: временное обращение товаров от величины товарооборота и т.д.

То есть как на микро-, так и на макро- уровне.

Классическим ее примером является кривая Филипса, характеризующая нелинейное соотношение между нормой безработицы Х и % прироста зарплаты У (у=а+(b/х)+ε).

Английский эксперт А.В.Филипс анализирует данные более чем за 100 летний период, в конце 50-х годов 20 века установил обратную зависимость процентного прироста зарплаты от уровня безработицы. Для равносторонней гиперболы всегда у=а+b/х +с, заменив 1/х=z, получим у=а+bz+с, оценка параметров, которая может быть дана МНК. Система нормального уравнения составит:

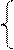∑у =na+b∑1/x

∑y/x=a∑1/x +b∑1/x²

При b>0 имеем обратную зависимость, которая при х → ∞ характеризуется нижней асимптотой, то есть минимальным предельным значением у, оценкой которого служит параметр а. Так для кривой Филипса ŷ_х=0,00697+0,1842 (1/х) величина параметра а=0,00697 означает, что с ростом уровня безработицы темп прироста зарплаты в пределе стремящимся к 0. Соответственно может определить тот уровень безработицы, при котором зарплата оказывается стабильной и темп ее прироста равен 0.

При b<0 имеем медленно повышающуюся функцию с верхней асимптотой при х→ ∞, т.е с максимальным предельным значением у, оценку которому в другом уравнении дает параметр а.

Примером может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (доходов). Математическое описание такого рода взаимосвязей получило название кривых Энгеля. В 1957 году нем. Статистик Э.Энгель на основе исследований семейных расходов сформулировал закономерность- с ростом дохода домашних доходов, расходуемых на продовольствие уменьшается соответственно с увеличением доходов доли доходов/расходов на непродовольственные товары будут возрастать. Однако, это увеличение не беспредельно, так как на все товары сумма долей не может быть больше 1 или 100%. А на отдельные непродовольственные товары этот предел может характеризоваться величиной параметра a уравнения вида: ,

где y – доля расходов на непроизводственные товары;

x - доля доходов на непроизводственные товары.

Вместе с тем равносторонняя гипербола не является единственной функцией для описания кривой Энгеля. В 1943 году Уоркинг и в 1964 году Лизер для этих целей использовали полулогарифмическую кривую

y = a+b lnx+e. Заменив lnx = Z получим линейное уравнение регрессии

y = a+bZ +e. Данная функция, как и предыдущая, линейна по параметрам и не линейна по объясняющей переменной x. Оценки параметров a и b могут быть найдены с помощью метода наименьших квадратов.

Система нормальных уравнений

Возможны и иные модели нелинейные по объясняющим переменным. Например, y = a+b +e. Соответствующие системы нормальных уравнений для оценки параметров составим:

Уравнение с квадратными корнями используют в исследовании урожайности, трудоемкости, сельскохозяйственного производства. В работе Н.Драйпера и Г.Смита справедливо отмечено, что если нет каких-либо теоретических обоснований в использовании данного вида кривых, то основная цель подобных преобразований состоит в том, чтобы для преобразованных переменных получить более простую модель регрессии, чем для исходных данных.

Иначе обстоит дело с регрессией не линейной по оцениваемым параметрам. Данный класс не линейных моделей подразделяется на два типа: 1. не линейные модели внутренне линейные;

2. не линейные модели внутренне не линейные.

Если не линейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же не линейная модель внутренне не линейна, то она не может быть сведена к линейной зависимости. Например, в экономический исследованиях при изучении эластичности спроса от цен, широко используется степенная функция y = a×x^b ×e,

где y – спрашиваемое количество; x – цена; e - случайная ошибка.

Данная модель не линейна относительно оцениваемых параметров так как включенные параметры a и b ………… Однако ее можно считать внутренне линейной так как логарифмирование по основанию e приводит его к линейному виду lny = lna+b lnx+lne. Соответствующие оценки параметров a и b могут быть найдены методом наименьших квадратов.

В рассматриваемой степенной функции предполагается, что случайная ошибка e мультипликативно связана с объясняющей переменной. Если же модель представить в виде y = a×x^b ×e, то она становится внутреннее не линейной так как ее невозможно привести к линейной.

Внутри не линейная модель вида y = a×x^b ×e или 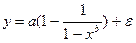, так как эти уравнения не могут быть преобразованы в уравнения не линейные по коэффициентам.

В специальных исследованиях по регрессионному анализу часто к не линейным относят модель внутренне не линейные по оцениваемым параметрам. А все другие модели, которые не линейны, но путем преобразования параметров они могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят экспонциональную модель y=e^a+bx + e, так как логарифмируя ее по натуральному основанию получим линейную форму модели lny=a+bx+lne.

Если модель внутренне не линейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Модели внутренне не линейные по параметрам могут иметь место в эконометрических исследованиях, но гораздо большее распространение получили модели, приводимые к линейному виду. Решение такого типа моделей реализовано в прикладных программ. Среди них в частности можно назвать и обратную модель вида: .

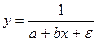Обращая обе части в равенства, получим линейную форму модели .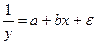

Приводима к линейному виду логическая функция

; .

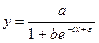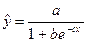Обращая обе части равенства, получим:

1+be^-cx+e = 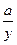; be^-cx+e = 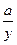-1

Прологарифмируя обе части по натуральному основанию получим уравнение линейной формы lnb-cx+e=ln(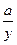-1);

Z=B-cx+e; Z=ln(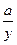-1); B= lnb

Среди не линейных функций, которые могут быть приведены к линейному виду в эконометрических исследованиях широко используется степенная функция y=ax^be. Связано это с тем, что параметр b имеет четкую эконометрическую интерпретацию, а именно является коэффициентом эластичности. Это значит, что величина коэффициента b показывает на сколько в среднем процентов изменится результат, если фактор изменится на 1%. Так, если зависимость спроса от уровня цен 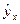=105,56×x^-1,12, то следует с увеличением цен на 1% спрос снижается на 1,12%. У равномерности подобной интерпретации параметра b для степенной функции можно судить, если рассмотреть формулу расчета

Э=¦¢(x) ,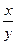

где ¦¢(x)- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.

Соответственно коэффициент эластичности окажется равным:

Э=abx^b-1×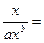bx^b-1×=b.

Коэффициент эластичности можно определить при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину равную параметру b. В других функциях коэффициент эластичности зависит от значения фактора x. Так для линейной регрессии 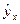=a+bx функция эластичности следующая:

¦¢(x)=b; Э=b×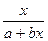

В силу того, что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения x, то обычно рассчитывают средний показатель эластичности по формуле: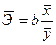

Для оценки параметров степенной функции y=ax^be применяется метод наименьших квадратов в логарифмированном уравнении lny=lna+blnx+lne, то есть решается система нормальных уравнений:

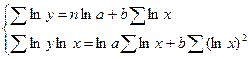
Параметр b определяется из системы, а параметр a – косвенным путем после потенцирования величины логарифма a. Так решая систему нормальных уравнений зависимости спроса от цен, было получено:

lny=4,6593-1,1214 lnx

после потенциации получим: 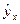=e^4,6593x^-1,1214=105,56x^-1,1214

Поскольку параметр a экономически не интерпретируется, то нередко зависимость записывается в виде логарифмически – линейной. В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно эластичность спроса характеризуется параметром b<0, эластичность предложения b>0.

Не смотря на широту использования в эконометрике коэффициентов эластичности возможны случаи, когда их расчет эконометрического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значения в процентах.

Например, вряд ли кто будет определять на сколько процентов может измениться заработная плата с ростом стажа работы на 1 %, или на сколько процентов изменится урожайность пшеницы, если качество изменится на 1%. В такой ситуации степенная функция даже если она окажется наилучшей по формальным соображениям (исходя из наименьшего значения остаточной вариации), не может быть эконометрически интерпретирована. Например, изучая соответствие ставок межбанковских кредитов y (процентных годовых) и срока его предоставления x (в днях) было получено уравнение регрессии: 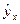=11,684×x^0,352.

С очень высоким показателем корреляции 0,9895, коэффициент эластичности 0,352% лишен смысла, так как срок предоставления кредита не измеряется в процентах. Значит больший интерес для этой зависимости может представить линейная функция: 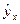=21,1+0,403x, имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает в процентных пунктах изменение ставок кредита с увеличением их предоставления на 1 день. При исчислении взаимосвязей среди функций, использующих lnx преобладают степенные зависимости – это кривые и спроса и предложения, и кривые Энгеля, и прощеные функции, и кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий и зависимость национального дохода от уровня занятости. В отдельных случаях может использоваться отдельная модель вида: y=. Так называемая обратная модель является разновидностью гиперболы. Но если в равносторонней гиперболе y=a++e преобразованию подвергается объясняющая переменная 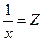, y=a+bZ+e то для получения линейной формы зависимости в обратной модели преобразуется x, , Z=a+bx+e

В результате обратная модель оказывается внутренне не линейной и преобразовывается методом наименьших квадратов, выполняется не для фактических значений признака, а для обратных величин 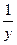, а именно .

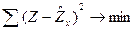Уравнение вида 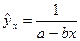характеризует прямую зависимость результативного признака от фактора. Оно целесообразно при очень медленном повышении результативного признака с ростом значения фактора. ……….. и одновременное исполнение логарифмических преобразований в обратные величины: y=e^{a-b x+e} .

Прологарифмирую, получим lny=a-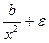, далее заменим 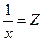и тогда для оценки параметров xлинейному уравнению lny=a-bZ+e может быть применен метод наименьших квадратов. При всех положительных значениях x функция возрастает. При x=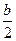кривая имеет точку перегиба, ускоренный рост при x>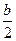. Подобного вида функции используются при анализе статистических данных о бюджетах потребителя, где выдвигается гипотеза о существовании асинтатического уровня расходов, об изменении предельной силе роста, о существовании «порогового уровня доходов». В этом случае при x®¥, y®e^a

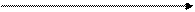
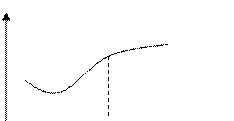функция насыщения

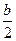x

При использовании линеризуемых функций, затрагивающих преобразование переменной y. Следует особенно проверять наличие предпосылок методом наименьших квадратов, чтобы они не нарушились при преобразовании. При не линейных соотношениях рассматриваемых признаков, приводимых к линейному виду, возможно интервальное оценивание параметров не линейной функции.

Для показателей на кривой сначала строятся доверительные интервалы для параметров нового преобразованного уравнения lny=lna+xlnb, то есть для lna и lnb. Далее с помощью обратного преобразования определяются доверительные интервалы для параметра b…..соотношении. В степенной функции доверительный интервал для параметра b строится так же ак и в линейной функции, то есть b ± t_xS_b. Отличие состоит лишь в том, что при определении стандартной ошибки параметров b используются не исходные данные, а их логарифмы:

S_b=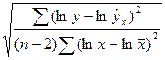

Заключение — до 5 мин.

Содержание и методические рекомендации:

- обобщить наиболее важные, существенные вопросы лекции.

- сформулировать общие выводы.

- поставить задачи для самостоятельной работы.

- ответить на вопросы студентов.

Дата добавления: 2014-01-14