Истечение из отверстий и насадков

Рассмотрим (рис.8-1) бак с жидкостью (например, водой), в днище которого есть отверстие (дырка).

Задача нестационарна, поскольку с течением времени, по мере вытекания жидкости, меняется скорость вытекания из дырки. Однако хочется рассматривать стационарный случай. Можно представить себе, что сверху над баком расположен кран, и из него в бак натекает столько же жидкости, сколько вытекает снизу.

С другой стороны, можно поставить условие, что площадь отверстия много меньше площади поперечного сечения бака: 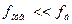Тогда уровень жидкости в баке будет понижаться очень медленно, и процесс можно приближенно считать стационарным.

Воспользуемся второй идеей и будем рассматривать истечение из узкого отверстия:

,

.

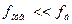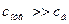Интересуемся скоростью истечения из дырки и объемным расходом.

Для нахождения скорости воспользуемся интегральным уравнением Бернулли, записав его для свободной поверхности бака и для сечения, где расположена дырка:

.

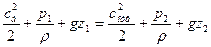Давление в сечениях «1» и «2» одинаково и равно атмосферному давлению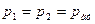

Это второе, после условия, наложенного на площади, допущение. Предполагаем, что высота бака не слишком велика, и разница в атмосферных давлениях, связанная с перепадом высот, отсутствует.

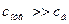, а в уравнение Бернулли скорости входят в квадрате, так что пренебрежем (третье допущение) удельной кинетической энергией на свободной поверхности бака: .

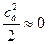Тогда можно записать:

.

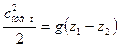Индекс «t» у скорости означает «теоретическая». Так исторически принято обозначать решения, полученные без учета трения.

Таким образом, теоретическая скорость истечения жидкости из малого отверстия определяется только высотой уровня жидкости в баке:

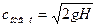(1) - формула Торричелли (была получена Торричелли еще в XVI веке).

Для того, чтобы учесть потери, связанные с вязкостью, необходимо провести численный расчет трехмерной задачи и сравнить результат с нашим решением.

Запишем так:

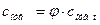, где 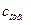- реальная скорость истечения,

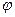- т.н. коэффициент скорости, безразмерная величина, меньшая единицы; зависит от формы отверстия и определяется по опытным данным.

Теперь определим объемный расход жидкости, вытекающей из отверстия. «Теоретический» расход (без учета трения) естественно определить через теоретическую скорость и площадь отверстия:

.

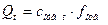Реальный расход найдем, умножая теоретический на коэффициент расхода ():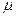

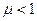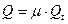(2)

Коэффициент расхода связан с коэффициентом скорости, учитывающем потери на вязкость, но определяется не только им.

Рассматривая истечение из узкого отверстия, мы подразумевали, хотя не оговаривали это особо, что отверстие удалено от боковых стенок бака (находится в центре), что позволяет пренебречь влиянием углов на процесс истечения (рис.8-2). Частицы жидкости вблизи дна, подходя к дырке, имеют значительную горизонтальную составляющую скорости. «Проваливаясь» в дырку, частица не может повернуть под прямым углом (поворот на нулевом радиусе означает бесконечно большую центробежную силу). Сила инерции отбрасывает частицы жидкости к оси струи, поэтому на малом расстоянии ниже отверстия струя сужается, площадь сечения струи уменьшается с 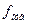до 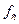; это явление называется сжатием струи. Для описания его вводят т.н. коэффициент сжатия , ().

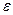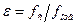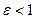Тогда истинный расход через отверстие

,

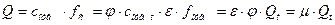так что коэффициент расхода выражается через произведение коэффициента сжатия струи и коэффициента скорости: .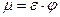

Коэффициент сжатия струи зависит от формы отверстия и толщины днища бака. Для отверстия с острыми кромками при достаточно толстой стенке (рис.8-3а) 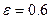. Если отверстие сделано с т.н. фасочкой, т.е. кромка сглажена (рис.8-3b), 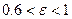. Коэффициент сжатия струи будет равен единице 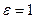, если форма отверстия точно подогнана под форму струи (рис.8-3с). Для баков с тонким днищем можно с целью увеличения 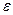(приближения к единице) приделать специальный патрубок, который называется насадком (рис.8-3d).

Дата добавления: 2014-01-14