Сходимость по вероятности. Закон больших чисел

Определение. Говорят, что последовательность с.в. {x _n } сходится по вероятности к с.в. x, если .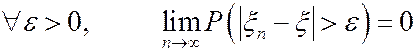

Обозначение: .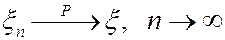

Лемма (признак сходимости по вероятности).

Если для последовательности с.в. {x _n } Мx _n =0, Dx _n ®0 при n ®¥, то .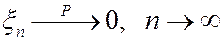

Пользуясь следствием из неравенства Чебышева и тем, что Мx _n =0, получим .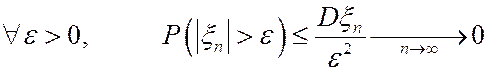

Теорема Чебышева.

Пусть {x _n } - последовательность попарно некоррелированных с.в., дисперсии которых ограничены в совокупности: Dx _i £ с i =1,2,…

Тогда последовательность с.в. 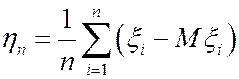сходится по вероятности к нулю при n®¥, то есть .

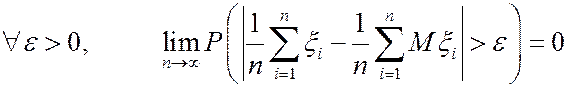Доказательство.

Имеем , .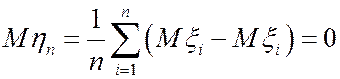

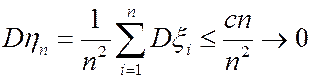Поскольку 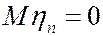, , то, в силу леммы, .

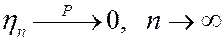Выше, при оценке дисперсии мы использовали тот факт, что для попарно некоррелированных с.в. x₁,…, x_n дисперсия от суммы равна сумме дисперсий.

Действительно,

.

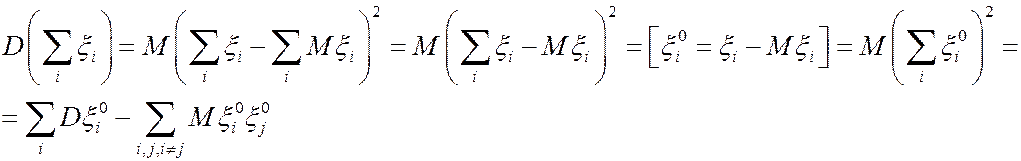Поскольку 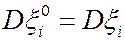и, по условию 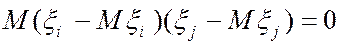, то

.

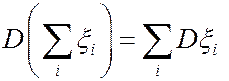Следствие 1. Пусть в условии теоремы Чебышева Мx _i = а, тогда последовательность с.в. 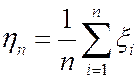сходится по вероятности к МО а, то есть .

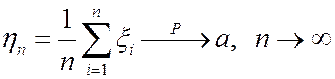Следствие 2. (теорема Бернулли). Пусть m_n –число успехов в серии из n испытаний Бернулли и р – вероятность успеха. Тогда последовательность частот (m_n/n) при n®¥ сходится по вероятности к р.

Действительно, .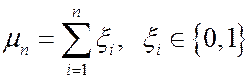

.

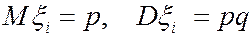Согласно следствию 1 последовательность с.в. 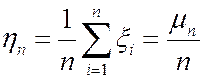сходится по вероятности к МО р.

Существуют теоремы, охватывающие более общие случаи, когда з.б.ч. выполняется. Рассмотрим 2 из них.

Теорема Маркова.

Если последовательность с.в. {x _n } такова, что и 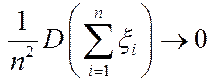при n®¥, то 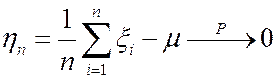при n®¥ (или, что тоже, ).

Заметим, что в теореме не требуется некоррелированности с.в.

Доказательство.

Поскольку Мh _n =0 и, согласно условию, Dh _n ®0 при n®¥, то, согласно лемме, получаем утверждение теоремы.

Можно иногда не требовать существования дисперсий у случайных величин.

Теорема Хинчина.

Пусть с.в. последовательности {x _n } одинаково распределены, независимы и имеют конечные МО m. Тогда 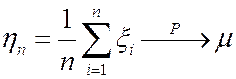при n®¥.

(Без док-ва).

3. Типы сходимости «почти наверное» и «в среднем квадратическом». Усиленный закон больших чисел.

То, что последовательность с.в. сходится по вероятности к какому-либо пределу, еще не гарантирует, что разность между пределом и членом последовательности с каким угодно номером достаточно мала. Иногда необходимо иметь более сильное определение сходимости, близкое к тому, которое используется при сходимости последовательности чисел.

Определение. Последовательность с.в. {x _n } сходится к с.в. x с вероятностью 1 (или «почти наверное») если 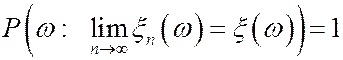. То есть множество тех w, для которых последовательность {x _n } сходится к с.в. x имеет вероятность 1.

Теорема (Усиленный з.б.ч.).

Пусть {x _n } - последовательность попарно независимых с.в. с конечными МО и дисперсиями; Mx _i =m, Dx _i =s². Тогда, при 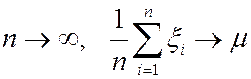с вероятностью 1.

(без док-ва)

Согласно приведенной теореме, случайная величина, представляющая частоту успехов, с вероятностью 1 сходится к вероятности успеха при числе испытаний n®¥.

В теории вероятностей встречаются и другие типы сходимости, например, сходимость «в средне квадратическом».

Определение. Последовательность с.в. {x _n } сходится к с.в. x в средне квадратическом при n®¥, если 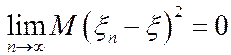. Обозначение: 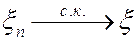или .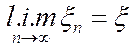

Типы сходимости почти наверное и в средне квадратическом более сильные типы сходимости, чем сходимость по вероятности.

Используя неравенство Чебышева 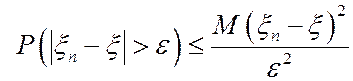, получим, что из сходимости в средне квадратическом следует сходимость по вероятности. Из сходимости почти наверное также следует сходимость по вероятности. Однако, между собой типы сходимости в средне квадратическом и почти наверное не связаны. Последовательность с.в. может сходиться почти наверное и не сходиться в средне квадратическом, или наоборот.

Дата добавления: 2014-01-14