Связь между линейным уравнением и системой линейных уравнений 1-го порядка

Введем новые функции

Теперь исходное линейное дифференциальное уравнение представляется в виде системы

Если ввести вектор-функцию 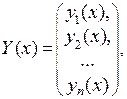систему легко записать в виде уравнения первого порядка: , где , .

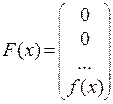Если для вектор-функции задать начальное условие: ,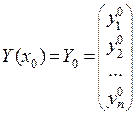

для полученного векторного дифференциального уравнения первого порядка с заданным начальным условием нетрудно доказать теорему существования и единственности решения соответствующей задачи Коши. Это решение так же, как в случае обыкновенного дифференциального уравнения первого порядка, может быть построено с помощью итераций интегрального уравнения 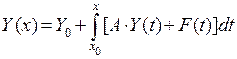в окрестности точки . Здесь интеграл от вектор-функции представляет собой новый вектор, каждая координата которого является интегралом соответствующей координаты исходной вектор-функции. Поскольку коэффициенты матрицы 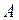– константы, то условие Липшица выполняется при всех значениях переменной x. Поэтому система дифференциальных уравнений первого порядка, к которой мы свели дифференциальное уравнение n -го порядка, при непрерывной функции 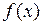разрешима и имеет единственное решение при любых начальных данных.

Из справедливости теоремы существования и единственности для системы следует справедливость теоремы существования и единственности для исходного линейного дифференциального уравнения n -го порядка: дифференциальное уравнение 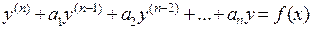с начальными условиями имеет единственное решение в окрестности точки .

Решение однородного уравнения.

Вследствие линейности дифференциального уравнения легко доказывается утверждение: есл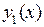и и 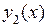– два частных решение уравнения 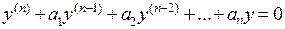, то при любых и – также решение этого уравнения.

Мы должны в виде общего решения однородного уравнения получить такую линейную комбинацию частных решений , чтобы было возможно получить решение соответствующей задачи Коши при любом наборе начальных условий . Это означает, что система

должна быть разрешима относительно набора констант при любой правой части, и значит, главный определитель системы отличен от нуля.

Рассмотрим определитель , называемый определителем Вронского. Именно условие позволяет удовлетворить заданным начальным условиям в точке .

Назовем систему частных решений уравнения

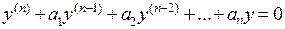линейно зависимой, если существуют такие числа 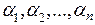, причем хотя бы одно из них отлично от нуля, что при всех значениях переменной x. В противном случае систему частных решений назовем линейно независимой. Очевидно, что определитель Вронского, составленный для линейно зависимой системы частных решений, тождественно равен нулю.

Утверждение. Если решения линейно независимы, то определитель Вронского , составленный для соответствующей системы частных решений, отличен от нуля при любых x.

Д о к а з а т е л ь с т в о. Предположим противное. Пусть найдется точка такая, что . Это означает, что система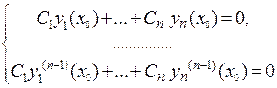

имеет нетривиальное решение . Следовательно, ненулевое решение исходного дифференциального уравнения n -го порядка удовлетворяет начальным условиям . Но при этом существует еще и тривиальное решение, удовлетворяющее тем же начальным условиям. Это противоречит теореме единственности.

Для того, чтобы получить систему линейно независимых решений, искать частное решение однородного уравнения будем в виде 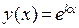. Подставив в указанном виде в однородное уравнение, получим . Следовательно, неизвестное значение сомножителя мы найдем, если решим алгебраическое уравнение 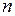-й степени

,

называемое характеристическим уравнением.

В соответствиисосновной теоремой алгебры характеристическое уравнение имеет ровно 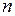корней, считая все вещественные и комплексные корни с учетом их кратности.

Рассмотрим все случаи корней характеристического уравнения и определим вид частного решения так, чтобы все частные решения были линейно-независимыми. Получив 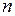линейно-независимых частных решений, мы сможем построить общее решение однородного уравнения , содержащее 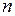произвольных постоянных и позволяющее решать любую задачу Коши с любыми начальными данными, сводя решение этой задачи Коши к системе с ненулевым главным определителем

.

а) Простой вещественный корень. Простому вещественному корню 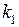характеристического уравнения соответствует частное решение . Если все корни характеристического уравнения простые и вещественные, определитель Вронского примет вид

.

П р и м е р. Решить однородное дифференциальное уравнение . Построим характеристическое уравнение . Это характеристическое уравнение имеет три простых корня: . Поэтому общим решение исходного дифференциального уравнение является функция .

Дата добавления: 2014-01-14