Частотные характеристики параллельного контура

Контур без потерь. Частотные зависимости параметров параллельного контура от частоты имеют вид:

B_L(w) = 1/(wL); B_C(w) = wC; B(w) = (1/wL) - wC; X(w) = 1/B(w). (12)

На рисунке 9.2 изображены графики этих зависимостей. Из рисунка следует: при w < w₀входное сопротивление контура Х носит индуктивный, а при w > w₀ёмкостной характер, причём вследствие отсутствия потерь при переходе через частоту w = w₀ ФЧХ контура изменяется скачком от -p/2 до p/2, а входное реактивное сопротивление контура претерпевает разрыв ( | Х| = µ).

Частотная зависимость входного тока определяется уравнением I(w) = U|B(w)|, т. е. является зеркальным отображением модуля реактивной проводимости В(w) (на рисунке 9.2 показано штриховой линией).

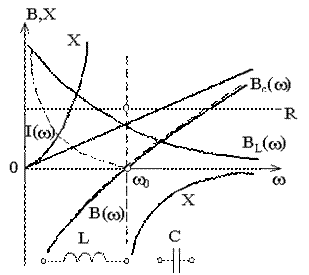
Рисунок 9.2 - Частотные зависимости параллельного контура без потерь

Контур с малыми потерями. Комплексное эквивалентное сопротивление контура можно определить уравнением:

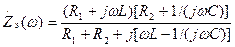. (13)

Выделяя активную R_Э и реактивную X_Э составляющие, получим уравнения частотных характеристик:

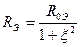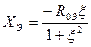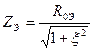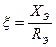; ; ; . (14-17)

На рисунке 9.3 изображены нормированные относительно R_0э частотные характеристики R_э/R_0э, X_э/R_0э и Z_э/R_0э как функции обобщенной расстройки x.

Рисунок 9.3 - Нормированные частотные характеристики параллельного контура

Фазочастотная характеристика цепи определится уравнением:

j = -arctg(X_э/R_э) = -arctgx. (18)

Анализ полученных зависимостей показывает, что по своему виду частотные характеристики контура с потерями существенно отличаются от характеристик контура без потерь. Это отличие касается, прежде всего, зависимости реактивного сопротивления контура от частоты: для контура с потерями при резонансе оно оказывается равным нулю, а в контуре без потерь терпит разрыв (см. рисунок 9.2).

Частотная зависимость токов I₁(w) и I₂(w) в ветвях определяется согласно закону Ома:

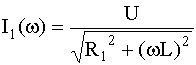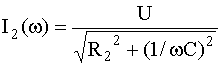; , (19, 20)

т. e. I₁ с увеличением w уменьшается, а I₂ растет, причем в пределе I₁(µ) = 0; I₂(µ) = U/R₂.

Колебательный контур подключается обычно к источнику с задающим напряжением 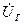и определённым внутренним сопротивлением R_Г. При этом напряжение на контуре определяется:

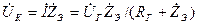. (21)

При резонансе токов: 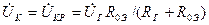. (22)

Определяя частотную зависимость 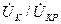и вводя понятие эквивалентной добротности контура

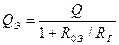, (23)

могут быть получены АЧХ и ФЧХ относительно напряжения на контуре, нормированного к напряжению U_КР:

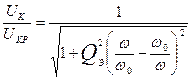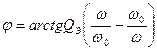; . (24, 25)

На рисунке 9.4 показан характер этих зависимостей при различных сопротивлениях R_Г источника.

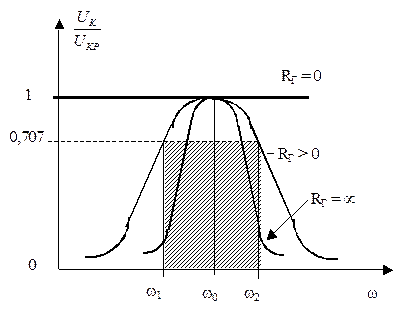
Рисунок 9.4 - Частотные характеристики параллельного контура

Полоса пропускания параллельного контура определяется как полоса частот, на границах которой напряжение на контуре уменьшается в 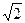раз относительно U_КР. Отсюда уравнения граничных частот полосы пропускания:

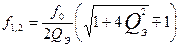; (26)

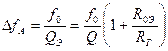(абсолютная полоса) (27)

Параллельный контур в общем случае имеет более широкую полосу, чем последовательный. И только при R_г = ¥ (см. рисунок 9.4) их полосы пропускания будут равны. Так образом, для улучшения избирательных свойств параллелью контура его необходимо возбуждать источником тока. Параллельный контур нельзя использовать для усиления напряжения, так как всегда U_к.р < U_г.

Электрические фильтры. Общие положения

Дата добавления: 2014-01-14