Параллельный колебательный контур и резонанс токов

Площадь треугольника, построенного на векторах и как на сторонах, численно равна половине модуля векторного произведения этих векторов.

Площадь параллелограмма, построенного на векторах и как на сторонах, численно равна модулю векторного произведения этих векторов.

Контрольные вопросы:

1. Какие три вектора называются правой тройкой векторов?

2. Какие три вектора называются левой тройкой векторов?

3. Сформулируйте определение векторного произведения векторов.

4. Какие свойства векторного произведения векторов Вам известны?

5. Как векторное произведение векторов выражается через их координаты?

6. Какие приложения векторного произведения векторов Вам известны?

Простейший параллельный колебательный контур с потерями в ветвях R ₁ и R ₂ имеет вид, изображенный на рисунке 9.1а.

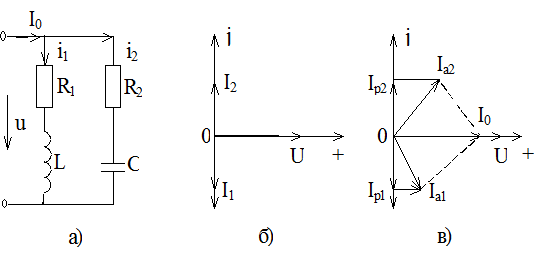
Рисунок 9.1 - Параллельный колебательный контур с потерями и векторные диаграммы

Комплексная входная проводимость такого контура:

Y = 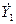+ 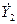= G ₁ + G ₂ - j(B ₁ - B ₂ ) = G - jB, (1)

где 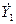= G ₁ - jB ₁; 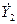= G ₂ - jB ₂ - комплексные проводимости ветвей с индуктивностью и емкостью соответственно.

Проводимости G₁, G₂, B₁, B₂ можно найти из формул преобразования:

G ₁ = R ₁/ Z ²₁; G ₂ = R ₂/ Z ²₂; B ₁ = wL / Z ²₁; B ₂ = (1/w C) / Z ²₂, (2)

где Z ₁ = 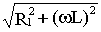; Z ₂ = .

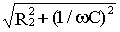Из условия резонанса токов имеем j = arctg (B/G) = 0. Отсюда следует:

B = B ₁ - B ₂ = {w L/[R₁² + (wL)²]} - { (1/wC)/[R₂² + (1/wC)²]} = 0. (3)

Решив (3) относительно w, получим уравнение резонансной частоты

w _p = . (4)

Резонанс в параллельном контуре возможен лишь в случае неотрицательности подкоренного выражения (т. е. при R₁ < r и R ₂ < r или R ₁ > r и R ₂ > r).

Реактивные составляющие токов в ветвях при резонансе равны друг другу:

I _p1 = UB ₁ = I _p2 = UB ₂. (5)

При этом ток в неразветвленной части цепи определяется из уравнения:

i₀ = U/R_0э, (6)

где активное сопротивление R_0э называют эквивалентным резонансным сопротивлением параллельного контура.

Входной ток контура совпадает по фазе с приложенным напряжением. Величину R_0э можно найти из условия резонанса токов. Так как при резонансе токов В = 0, то полная эквивалентная проводимость контура:

G_0э = G₁ + G₂ = 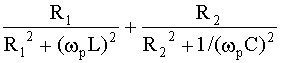. (7)

Подставив значение w_р, получим G_0э = (r₁ + R₂)/(r² + R₁R₂), откуда:

R_0э = (r ² + R₁R₂)/(R₁ + R ₂). (8)

Наибольший теоретический и практический интерес представляют резонанс токов в контурах без потерь и с малыми потерями.

Контур без потерь. Для контура без потерь (R₁ = R₂ = 0)уравнение резонансной частоты принимает вид:

w_р = w₀ = 1/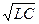, (9)

т. е. совпадает с выражением для последовательного контура.

Эквивалентное сопротивление контура без потерь R_0э = µ и входной ток равен нулю, а добротность обращается в бесконечность.

Сумма энергий электрического и магнитного полей для параллельного контура без потерь, как и для последовательного контура, остается неизменной.

Контур с малыми потерями. (R₁ << r; R₂ << r ).Резонансная частота для этого случая будет приближенно совпадать с частотой w₀. Для контура с малыми потерями можно принять, что r² >> R₁R₂, тогда:

R_0э» r ²/(R₁ + R₂) = r ²/R = Q²R, (10)

где R = R₁ + R₂.

Ток в неразветвленной части цепи: I₀ = U/R_0э = U/(Q²R), а действующие значения токов в ветвях:

I₁ = I₂ = U/r = U/(QR). (11)

То есть, отношение токов в ветвях к току в неразветвленной части цепи равно добротности контура: I₁/I₀ = I₂/I₀ = Q, т. е. ток в реактивных элементах L и С при резонансе в Q раз больше тока на входе контура (отсюда термин “резонанс токов”). На рисунке 9.1визображена векторная диаграмма токов для этого случая. В контуре с потерями сумма энергий электрического и магнитного полей не остается постоянной.

При R₁ = R ₂ = r для w_р получаем неопределенность, при этом входное сопротивление контура будет носить чисто активный характер на любой частоте (случай безразличного резонанса).

Дата добавления: 2014-01-14