Механические свойства металлов. Основными механическими свойствами металлов являются прочность, упругость, пластичность, твердость и вязкость

Основными механическими свойствами металлов являются прочность, упругость, пластичность, твердость и вязкость.

Уровень механических свойств металлов определяют испытанием специальных образцов.

При испытании на растяжение определяют. предел пропорциональности, предел упругости, предел текучести, временное сопротивление (предел прочности), истинное сопротивление разрыву, относительное удлинение после разрыва, относительное сужение после разрыва.

При растяжении образца в испытательной машине записывающий прибор вычерчивает диаграмму растяжения (рис. 6. а). Она показывает зависимость деформации образца от растягивающей нагрузки.

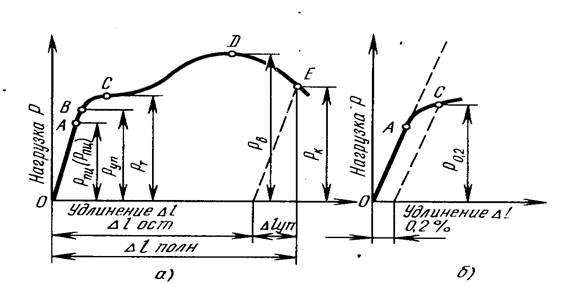
Рис.6. Диаграмма растяжения образца на низкоуглеродистой стали (а) и схема определения условного предела текучести (б)

На этой диаграмме по оси ординат откладывается нагрузка Р, а по оси абсцисс абсолютное удлинение образца Δl. От начала деформации точки О и до точки А образец деформируется пропорционально приложенной нагрузке. Участок ОА представляет прямую линию. Если нагрузку Р_пц снять, то полученная образцом деформация исчезнет, и образец примет первоначальные размеры. Если же нагрузку увеличить, то начнется отклонение линии ОА от прямолинейного направления. Таким образом, нагрузка Р_пц является предельной, до которой сохраняется пропорциональность между прилагаемой нагрузкой и деформацией образца. Закон прямой пропорциональности носит название закона Гука: относительная линейная деформация ε прямо пропорциональна соответствующему нормальному (действующему перпендикулярно площади) напряжению δ, т. е. ε = δ/E Величина Е характеризует способность металла сопротивляться упругому деформированию. Эта величина называется модулем упругости первого рода или модулем Юнга. Е выражается в единицах силы на единицу площади (Н/м²) (кгс/мм²). Различные металлы имеют различную жесткость, т. е. различную величину модуля упругости. У стали Е находится в пределах (20-21) ×10⁴ у латуни - (10-11) ×10⁴ у алюминиевых сплавов - (7-8) ×10⁴ Н/мм².

Предел пропорциональности δ_пц (Н/мм²) представляет напряжение, выше которого нарушается пропорциональность между прилагаемым напряжением и деформацией образца: δ_пц = Р_пц / F_o), где F_o - площадь поперечного сечения образца.

Выше точки А располагается точка В, ордината которой соответствует нагрузке, вызывающей определенное остаточное удлинение образца: если снять нагрузку, длина образца будет больше начальной. Для практических целей величину этого остаточного удлинения принимают равной 0,05% от начальной расчетной длины образца. Напряжение, при котором остаточное удлинение достигает 0,05% от начальной расчетной длины образца, называют условвым пределом упругости δ_0,05. При дальнейшем увеличении нагрузки до Р_т (точка С) на диаграмме появляется криволинейный участок, который при испытании мягких материалов может перейти в горизонтальную площадку. Это показывает, что даже незначительное увеличение нагрузки вызывает деформацию, «текучесть», образца. После снятия нагрузки образец сохраняет остаточную деформацию. Предел текучести (физический) - наименьшее напряжение, при котором образец деформируется без заметного увеличения нагрузки. Нагрузку Р_T можно определить по остановке стрелки силоизмерительного устройства испытательной машины, вызванной деформацией образца без заметного увеличения нагрузки. Предел текучести δ, Н/м² (физический) вычисляют по формуле δ =Р_T/F_o.

При испытании большинства металлов горизонтальная площадка на диаграмме отсутствует. В этих случаях определяют предел текучести условный δ_0,2 - напряжение, при котором остаточное удлинение достигает 0,2% от начальной расчетной длины образца. Предел текучести δ_0,2 (Н/м²) (кгс мм²) вычисляют по формуле: δ_0,2 = P_0,2/F_o.

Для определения нагрузки Р_0,2 (рис. б, б) на оси абсцисс от точки О вправо в соответствующем масштабе откладывают отрезок, равный 0,02% начальной расчетной длины образца, и проводят линию, параллельную ОА, до пересечения с диаграммой растяжения (точка С). Точка С определяет высоту ординаты, т. е. нагрузку Р_0,2, отвечающую пределу текучести. При дальнейшем увеличении нагрузки до Р_B (точка D) у пластичных металлов происходит равномерная деформация образца по длине и поперечному сечению, а образцы из хрупких металлов при этой нагрузке разрушаются.

Напряжение, соответствующее наибольшей нагрузке Р_max, предшествующей разрушению образца, называется временным сопротивлением

δ_B (Н/м²) (кгс/мм²) и вычисляется по формуле δ_B =Р_max/F_o. Для хрупких металлов δ_B характеризует сопротивление разрушению, а для пластичных металлов - сопротивление большим пластическим деформациям.

Далее нагрузка уменьшается. Это связано с тем, что у пластичного металла начинается местное сужение поперечного сечения (образуется шейка). И в точке Е образец разрушается.

У пластичных материалов, получающих заметную пластическую деформацию при растяжении, есть еще одна характеристика - истинное сопротивление разрыву S_k (Н/м²) (кгс/мм²). Это напряжение, определяемое отношением нагрузки Р_к в момент разрыва к площади минимального поперечного сечения образца после разрыва F_k: S_к=Р_к/F_к.

Пластичность металла при разрыве определяют по двум характеристикам: относительному удлинению и относительному сужению.

Относительное удлинение после разрыва δ (%) - отношение удлинения расчетной длины образца (l_к-l_o) после разрыва к ее первоначальной длине l_o: δ =(l_к – l_o)/ l_o

Относительное сужение после разрыва - отношение разности начальной площади и минимальной площади поперечного сечения образца после разрыва к начальной площади поперечного сечения образца:

φ = (F_o – F_к/F_o) × 100%

Дата добавления: 2014-01-14