Реальные и критические изотермы

График уравнения ван-дер-ваальса

Кривая уравнения Ван-дер-Ваальса при невысоких температурах имеет вид, показанный на рис. 88. Правая часть участка об весьма близка к изотерме закона Бойля— Мариотта. Действительно, при большом объеме газа обе поправки в уравнении Ван-дер-Ваальса невелики и левая часть уравнения близка к значению pV. По мере уменьше­ния объема поправки начинают играть заметную роль, При некотором объеме, которому соответствует точка б на графике, газ при обычных условиях начинает конденсиро­ваться, образуется двухфазная система жидкость — насы­щающий пар. Давление насыщающих паров зависит только от температуры, поэтому пока весь пар не превратится в жидкость, давление изменяться не будет, процесс конден­сация изобразится изобарой — прямой бд, параллельной оси абсцисс. Точка д изображает окончание процесса конденсации: весь насыщающий пар превратился в жидкость. Дальнейшее очень незначительное уменьшение объема жид­кости может быть получено лишь значительным увеличением давления, поэтому линия де, изображающая жидкое сос­тояние, идет круто вверх. Точки прямой бд, за исключением точки пересечения ее с кривой вг, не описываются уравнением Ван-дер-Ваальса. Кривая бвгд изображает малоустойчивые или вовсе неустойчивые состояния вещества. При изотермическом расширении точки д и б соответствуют началу и концу кипения. Точка д соответствует кипящей жидкости, точка б – сухому насыщенному пару. Смесь кипящей жидкости и сухого насыщенного пара, которая существует в любой точке участка д б, называется влажным паром.

На рис. 24 приведены экспериментальные изотермы реального газа. Они отличаются от изотерм Ван-дер-Ваальса (см. рис. 23). Последние при низких температурах имеют минимумы (точка г) и максимумы (точка в). При некоторой (критической) температуре Т_кр на изотерме имеется только точка перегиба К. При высо­ких температурах (Т > Т_кр) изотермы Ван-дер-Ваальса по­хожи на изотермы идеального газа. На экспериментальных изотермах отсутствуют "волнообразные" участки. Вместо них у реальных изо­терм имеется прямолинейный горизонтальный участок. Рассмотрим более подробно изотермы при Т₄ (см. рис 24). Участок а-в изотермы Ван-дер-Ваальса и участок 1-2 реальной изотермы практически одинаковы. Это состояние нена­сыщенного пара. Изотермы Ван-дер-Ваальса и реальные ведут себя различным образом в области расслоения на две фазы. Расслоение на две фазы объясняется неустойчивостью од­нородных состояний, отвечающих завитку бвгд (см.рис.3). Состояния, соответствующие участкам бв и гд, при известных условиях могут осуществляться. Однако эти со­стояния неустойчивы. Достаточно на участке бв попадания в пар пылинки, чтобы все вещество распалось на две фазы и пе­решло в состояние, изображаемое прямой 2-6 на рис. 24. Подобное состоя­ние называется метастабильным. Вещество в состоянии гд на­зывается пересыщенным паром.

На рис. 24 приведены изотермы для нескольких значений температуры. Из рисунков видно, что волнообразный участок 2-6 теоретической изотермы (рис. 23) и горизонтальный участок эксперимен­тальных изотерм (рис. 24) сокращаются с повышением темпера­туры и при критической температуре Т_кр стягиваются в точку. При критической температуре полностью исчезает всякое раз­личие между жидкостью и паром. Точка К называется кри­тической точкой. Критическая температура Т_кр — это такая тем­пература, выше которой газ нельзя превратить в жидкость никаким давлением, а ниже которой газ можно превратить в жидкость при некотором давлении, тем меньшем, чем ниже тем­пература. Объем V_кр и давление р_кр, соответствующие кри­тическому состоянию, называются критическими величинами. Из рис 24 видно, что давление насыщенного пара растет с температурой (точка 2 на каждой кривой), достигая при кри­тической температуре значения р_кр. При температурах выше критической понятие насыщенного пара теряет смысл.

Если провести линию через точки 2 и 6 соответственно на каждой изотерме (рис. 25), получается колоколообразная кривая. Она ограничивает об­ласть двухфазных состояний вещества. Эта кривая и участок критической изотермы (рис. 25), лежащий слева от точки -К, делит диаграмму (р, V) на три области. Область Ж — область однородных жидких состояний вещества. Область П + Ж — это область двухфаз­ных состояний. Область Г — область однородного газообразного вещества. В последней можно выделить участок П, который на­зывается областью пара. Вещество, находящееся в таком состоя­нии, при изотермическом сжатии превращается в жидкость. Решение уравнения (3) дает

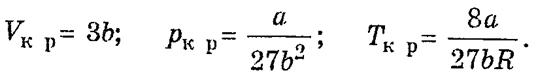(3. 6)

Таким образом, зная константы Ван-дер-Ваальса а и b, можно найти соответствующие критической точке величины коэффициенты а и b в уравнении Ван-дер-Ваальса и универсальную газовую постоянную R.

Р_к = ,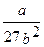

V_mк =3b,

Т_к = ;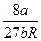

Дата добавления: 2014-01-14