Теплопроводность газов

Отсюда

Справа налево перенесено количество движения

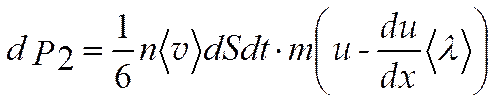(4.11)

Полное изменение количества движения, dK = dK₂-dK₁, равно импульсу, переданному от одного слоя газа к другому:

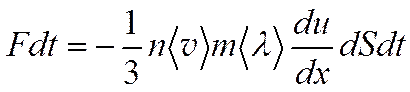(4.12)

(4.13)

Сравнивая (4.5) с формулой Ньютона (1), получим выражение для коэффициента внутреннего трения:

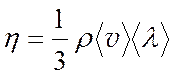(4.14)

Подставив вместо l выражение для длины свободного пробега <l> = 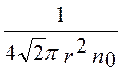, получим

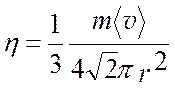(4.15)

Отсюда видно, что коэффициент внутреннего трения для газов не зависит от числа молекул в единице объема, т. е. он не зависит от давления и плотности газа. Это очень важ­ный результат. Можно менять давление в весьма широких пределах, а коэффициент внутреннего трения газа будет оставаться постоянным.

Это положение, однако, становится неверным для силь­но разреженных газов, т. е. для таких газов, у которых длина свободного пробега молекулы больше, чем линейные размеры, сосуда, в котором заключен газ. В этом случае молекулы движутся от одной стенки сосуда до другой, не сталкиваясь друг с другом, длина свободного пробега l оказывается постоянной величиной, и формула (4.15) для расчета h становится неверной.

Мы предположили, что все молекулы имеют одинаковую среднюю скорость и. Если произвести более строгий рас­чет, учитывая максвелловское распределение скоростей, то вместо коэффициента 1/3 в формулах (5) и (6) поя­вится коэффициент 0,31.

Рассмотрим газ, заключенный между двумя поверхнос­тями, имеющими температуры T₁ и Т₂. Если эти темпера­туры поддерживаются постоянными, то через газ установит­ся стационарный поток теплоты. Для простоты, чтобы рассматривать од­номерную задачу, помес­тим газ между двумя параллельными поверхнос­тями и ось Х направим перпендикулярно к этим поверхностям. Тогда вдоль оси Х будет градиент температуры 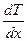, вдоль осей У и Z, располо­женных параллельно к ограничивающим газ поверхностям, температура не меняется. Рассмотрим поток теплоты через пло­щадку dS = dydz, помещенную перпендикулярно к оси Х (рис. 29).

Температура в точке К, находящейся слева от площадки dS на расстоянии, равном средней длине свободного пробега молекулы 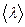, равна

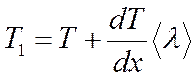; (4.16)

Дата добавления: 2014-01-14