Побудова лінії перетину двох площин

Лінія перетину двох площин – це їхня спільна пряма лінія. Вона визначається двома спільними для заданих площин точками або однією спільною точкою і напрямком. Напрямок лінії перетину відомий, якщо одна із двох площин, що перетинаються, проходить через пряму, яка належить другій площині (лінія перетину збігається з цією прямою), або якщо одна із площин паралельна якійсь прямій другої площини (лінія перетину паралельна цій прямій).

Методика побудови лінії перетину двох площин залежить від розташування їх щодо площин проекцій. Можна навести чотири характерні випадки:

- обидві площини різнойменно проекціювальні (рис. 4.7);

- обидві площини однойменно проекціювальні (рис. 4.8);

- одна площина окремого положення, а друга – загального (рис. 4.9);

- обидві площини загального положення (рис. 4.10).

У першому випадку (рис. 4.7) визначення лінії перетину площин полягає у розпізнанні та позначенні її проекцій, які збігаються зі слідами-проекціями заданих площин: l₁ = Ω₁, l₂ = F₂.

Якщо обидві площини перпендикулярні до якоїсь площини проекцій, то і лінія їхнього перетину також перпендикулярна до цієї ж площини проекцій (рис. 4.8): Λ(Λ₁) ^ П₁, Θ(Θ₁) ^ П₁, Λ ∩ Θ = m ^ П₁.

У разі, коли одна із площин загального положення, а друга – окремо

го, то одна із проекцій лінії їхнього перетину збігається з відповідним слідом-проекцією площини окремого положення. Друга проекція лінії пере

Рис. 4.7 Рис. 4.8 Рис. 4.9 Рис. 4.10

тину визначається за умови належності її площині загального положення. На рис. 4.9 показано дві площини: горизонтально проекціювальна Σ(Σ₁) і загального положення Ψ(ΔMNP). Горизонтальна проекція n₁ їхньої лінії перетину збігається зі слідом-проекцією Σ₁(S₁=n₁), а фронтальна n₂ знаходиться за допомогою точок 1(1₁, 1₂) і 2(2₁, 2₂), що належать сторонам MP(M₁P₁, M₂P₂) і MN(M₁N₁, M₂N₂) трикутника MNP.

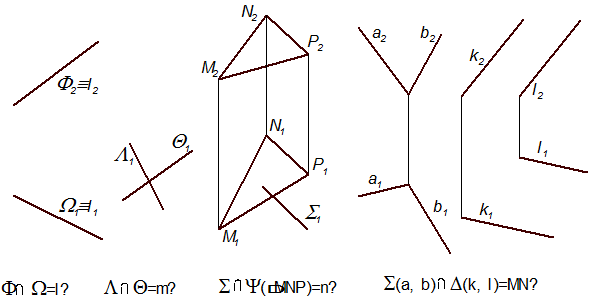Лінію перетину двох площин загального положення доцільно будувати за допомогою двох площин-посередників за таким алгоритмом (рис. 4.11):

1) задані площини Γ і Δ перетинаються допоміжною площиною-посередником Σ;

2) будуються дві лінії перетину заданих площин з площиною-посередником: 12 = Σ ∩ Γ, 34 = Σ ∩ Δ;

3) відмічається точка перетину побудованих ліній перетину:

М = 12 ∩ 34;

4) площини Γ і Δ перетинаються другою площиною-посередником Ψ;

5) будуються дві лінії перетину площини Ψ із заданими:

56 = Ψ ∩ Γ, 78 = Ψ ∩ Δ;

6) відмічається точка перетину побудованих ліній:

N = 56 ∩ 78.

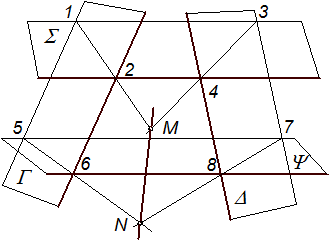Пряма, що проходить через точки M i N, є лінією перетину заданих площин Γ і Δ.

Може виявитися, що перша площина-посередник перетинає задані площини по паралельним прямим. Це може свідчити про те, що площини паралельні між собою, або площина-посередник паралельна їхній лінії перетину. У такому разі другу площину-посередник слід провести не паралельно першій. Якщо і друга площина- Рис. 4.11

посередник перетинає задані

площини по паралельним прямим, то ці площини паралельні. Якщо ж друга площина –посередник перетинає задані площини по не паралельним прямим, то через точку перетину цих прямих проходить лінія перетину заданих площин паралельно прямим перетину першої площини-посередника із заданими площинами.

Складність та точність побудови лінії перетину площин залежить від вибору площин-посередників. Розглянемо декілька прикладів. На рис. 4.12 показано побудову лінії перетину площин Γ(a; b) і Δ(k || l). Задані площини перетнуто горизонтальною площиною-посередником Σ(Σ₂). Для підвищення точності побудови її слід проводити подалі від точки 5(5₁, 5₂) перетину прямих a і b площини Γ. Площина Σ перетинає площину Γ по прямій 12(1₁2₁, 1₂2₂), а площину Δ – по прямій 34(3₁4₁, 3₂4₂). У перетині проекцій 1₁2₁ і 3₁4₁ цих прямих знайдено горизонтальну проекцію М₁ точки М спільної для площин Г і Δ. За лінією зв’язку знайдена фронтальна проекція М₂ цієї точки (M₂ Ì S₂).

Далі площини Γ і Δ перетнуто другою площиною-посередником Ψ(Ψ₂), яку проведено через точку 5(5₂) перетину прямих a і b площини Г паралельно площині-посереднику Σ(Σ₂). У такому разі площина Ψ перетинає площину Г по прямій 5N(5₁N₁), яка Рис. 4.12

паралельна прямій 12(1₁2₁), а площину Δ – по прямій 67(6₁7₁), паралельній прямій 34(3₁4₁). У перетині цих прямих маємо точку N(N₁), за лінією зв’язку знаходимо її фронтальну проекцію N₂ (N₂ Ì Y₂). Через точки М(М₁, М₂) і N(N₁, N₂) проводимо пряму MN. Це і є лінія перетину площин Γ і Δ.

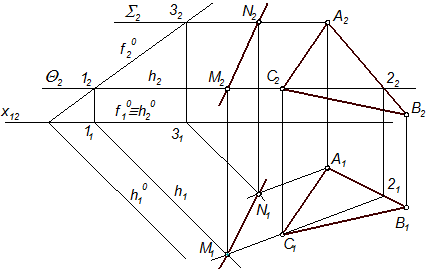На рис. 4.13 показано побудову лінії перетину двох площин Δ(fº, hº), поданої слідами, та Λ(ΔАВС). Першу горизонтальну площину-посередник Θ(Θ₂) проведено через вершину С(С₂) трикутника. Вона перетинає площину Δ по її горизонталі h(h₁, h₂), яка проходить через точку 1(1₁, 1₂) перетину площини Θ з фронтальним слідом f°(f°₂) площини Δ, а площину Λ - по прямій 2С(2₁С₁, 2₂С₂). У перетині прямих h та 2C маємо точку М(М₁, М₂): h₁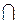2₁C₁ = M₁, M₂ = Q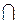₂ M₁M₂.

Другу горизонтальну площину-посередник Σ(Σ₂) проведено через вершину А(А₂)

трикутника АВС. Вона перетинає площину Рис. 4.13

Δ по її горизонталі

(не позначена), яка проходить через вершину А(А₁, А₂) паралельно прямій 2С, а площину D - по прямій 3N. У перетині цих прямих знаходимо точку N(N₁, N₂): A₁N₁ || 2₁C₁, 3₁N₁ || h₁, A₁N₁ ∩ 3₁N₁ = N₁. Фронтальна проекція N₂ точки N знайдена за лінією зв’язку: N₂ Ì S₂. Пряма MN(M₁N₁, M₂N₂) є лінією перетину площин Δ і Λ.

На рис. 4.14 показано побудову лінії перетину двох трикутних відсіків площин загального положення. Проекції відсіків накладені одна на одну. У цьому разі площини-посередники доцільно проводити через сторони трикутників. Першу площину-посередник Σ(Σ₂) проведено через сторону АВ(А₁В₁, А₂В₂) трикутника АВС. Сторона АВ є лінією

Рис. 4.14

перетину площини Σ з площиною трикутника АВС. Площину трикутника DEF(D₁E₁F₁, D₂E₂F₂) площина Σ перетинає по прямій 12(1₁2₁, 1₂2₂): 1 = Σ ∩ EF, 2 = Σ ∩ DF. Пряма 12 перетинає сторону АВ у точці М(М₁, М₂): 1₁2₁ ∩ А₁В₁ = М₁. Проекція М₂ знайдена за лінією зв’язку: M₂ Ì A₂B₂.

Друга площина-посередник Ψ(Ψ₂) проведена через сторону АС(А₁С₁, А₂С₂) трикутника АВС. Ця площина перетинається з трикутником DEF по прямій 34(3₁4₁, 3₂4₂), а з трикутником АВС – по прямій АС. У перетині прямих АС і 34 маємо точку N(N₁, N₂): 3₁4₁ ∩ А₁С₁ = N₁, N₂ = A₂C₂ 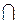N₁N₂. Лінія MN(M₁N₁, M₂N₂) – це лінія перетину площин відсіків. ЇЇ відрізок МК(М₁К₁, М₂К₂) знаходиться в межах обох відсіків. Таку побудову лінії перетину площин можна витлумачити і як побудову цієї лінії за двома точками М і N перетину сторін АВ і АС трикутника АВС з площиною трикутника DEF. Таке тлумачення зустрічається у деяких підручниках та посібниках.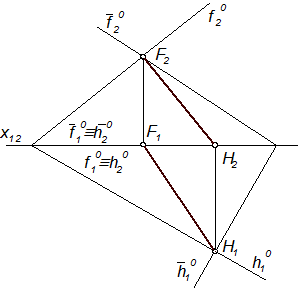

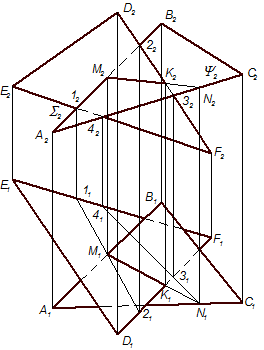
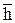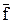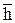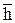Лінію перетину двох площин, поданих своїми слідами, доцільно знаходити за точками перетину слідів цих площин, якщо вони не виходять за межі креслення. У цьому разі роль площин-посередників відіграють площини проекцій, яким належать сліди площин. Так, на рис. 4.15 показано побудову лінії перетину двох площин Γ(hº, fº) і Δ(º, º). Горизонтальні сліди hº(hº₁, hº₂) i º(º₁,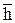º₂) перетинаються у точці Рис. 4.15

Н(Н₁, Н₂), а фронтальні fº(fº₁, fº₂) та

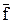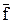º(º₁, 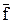º₂) – у точці F(F₁, F₂). Пряма HF(H₁F₁, H₂F₂) є лінією перетину площин Г і Δ, а точки H і F – це її сліди.

Дата добавления: 2014-01-14