Перетин прямої з площиною

Задача на побудову точки перетину прямої з площиною є першою основною позиційною задачею. Точка перетину прямої з площиною – це точка, яка є спільною для прямої і площини. Вона може бути визначеною на будь-яких двох проекціях прямої і площини. Третя проекція цієї точки може бути побудованою за методикою, розглянутою у п. 1.3.

Визначення точки перетину прямої з площиною залежить від розташування прямої і площини щодо тих площин проекцій, на полях яких визначається ця точка. Можна навести чотири характерні випадки:

- пряма і площина різнойменно проекціювальні;

- площина проекціювальна, а пряма загального положення;

- пряма проекціювальна, а площина загального положення;

- пряма і площина перебувають у загальному положенні.

У першому випадку (рис. 4.16) обидві проекції точки перетину уже є на кресленні. Визначення цієї точки зводиться до розпізнання і позначення її проекцій: горизонтальна проекція М₁ точки М збігається з проекцією l ₁ прямої l, а фронтальна знаходиться у перетині l₂ прямої l та Г₂ площини Г.

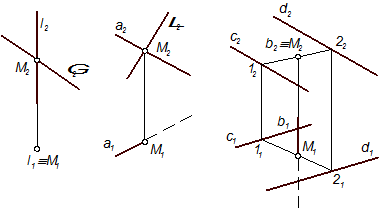У другому випадку (рис. 4.17) одна проекція точки перетину – точка перетину проекцій прямої і площини (М₂ = а₂∩Λ₂), а друга знаходиться за лінією зв’язку за умови належності її прямій:

М₁Îа₁. У цьому разі

на одній із проекцій точка перетину поділяє пряму на видиму і невидиму

частини. Невидиму частину, яку закриває від спостерігача задана площина, слід зображувати Рис. 4.16 Рис. 4.17 Рис. 4.18

штриховою лінією.

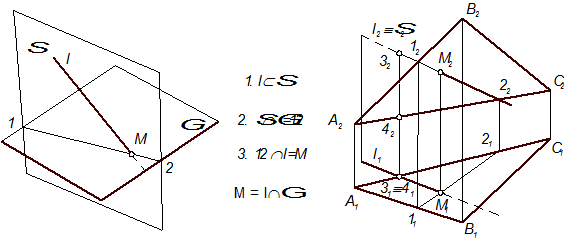У третьому випадку (рис. 4.18) одна з проекцій шуканої точки збігається з проекцією прямої (b₂ = M₂), а друга будується за умови належності її заданій площині за допомогою будь-якої прямої 12(1₁2₁, 1₂2₂), що належить цій площині: М₂ Î 1₂2₂ (1₂Îс₂, 2₂ Î d₂), M₁ = b₁ ∩ 1₁2₁ (1₁ Îc₁, 2₁ Î d₁).

У четвертому випадку точку перетину прямої з площиною будують за такими міркуваннями. Точка перетину (рис. 4.19) належить прямій l і площині Г, отже вона належить якійсь прямій площини Г, що перетинається з даною прямою l. Тому у заданій площині необхідно знайти таку пряму, яка перетинається з прямою l. Перетинаються між собою тільки ті

Рис. 4.19 Рис. 4.20

прямі, що належать одній площині. Тож через задану пряму l проводять яку-небудь допоміжну площину S і будують лінію 12 перетину її із заданою площиною Г. Точка М перетину заданої прямої l і побудованої прямої 12 – це точка перетину прямої l з площиною Г, оскільки вона належить і прямій l і прямій 12, інцидентній площині Г.

Тут може виникнути три різні ситуації:

- побудована лінія перетину 12 збігається із заданою прямою, це означає, що задана пряма належить заданій площині;

- побудована пряма 12 паралельна заданій прямій l, це означає, що задана пряма l паралельна заданій площині;

- побудована лінія 12 перетинає пряму l, у цьому разі пряма l перетинається з площиною.

Тому алгоритм побудови точки перетину прямої з площиною може використовуватись для визначення взаємного положення заданих прямої і площини.

Допоміжну площину S слід так проводити через пряму l, щоб побудови були найпростішими і забезпечували найточніший результат. Найчастіше через пряму проводиться проекціювальна площина, але може бути використана і площина загального положення, наприклад, у разі, якщо пряма – профільна.

На рис. 4.20 показано побудову точки перетину прямої l (l ₁, l ₂) з площиною Г(DАВС). Через пряму l проведена допоміжна фронтально проекціювальна площина S(S₂), яка перетинає площину Г по лінії 12(1₁2₁, 1₂2₂): S∩АВ = 1, S∩АС = 2. У перетині прямої l (l ₁) з прямою 12(1₁2₁) маємо точку М(М₁). За лінією зв’язку знаходимо її фронтальну проекцію М₂: М₂ Î l ₂. Точка М поділяє пряму l на дві частини – видиму і невидиму (з огляду на те, що площина Г не обмежена трикутником АВС). Видимість прямої l на фронтальній і горизонтальній проекціях можна встановити за уявленням або за допомогою конкуруючих точок. На горизонтальній проекції це зроблено за допомогою точок 3 Î l і 4 Î АС: тобто пряма l зіставлена зі стороною АС трикутника.

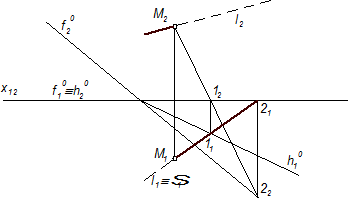У точці перетину горизонтальних проекцій l ₁ і А₁С₁ збігаються горизонтальні проекції 3₁ і 4₁ точок 3 і 4. На фронтальній проекції видно, що точка 3(3₂) розташована вище, ніж точка 4(4₂). Це означає, що пряма l проходить над прямою АС. Отже, пряма l зліва від точки М на горизонтальній проекції видима, а справа – невидима. Аналогічно визначена видимість прямої l і на фронтальній проекції. Рис. 4.21

На рис. 4.21 показано побудову точки перетину прямої l (l ₁, l ₂) з площиною Q(h°, f°). Через пряму l проведена горизонтально проекціювальна площина S(S₁), яка перетинає площину Q по прямій 12(1₁2₁, 1₂2₂): 1 = h° ∩ S (1₁ = h°₁ ∩ S₁), 2 = f° ∩ S (2₁ = f₁° ∩ S₁); 1₂ Î h₂°, 2₂ Î f₂°. Пряма 12 перетинає пряму l у точці М(М₁, М₂): 1₂2₂∩ l ₂ = M₂, M₁Î l ₁.Точка М і є точкою перетину прямої l з площиною Q. Видимість прямої визначається співставленням її частин зі слідами площини. Так, частина прямої l зліва від точки М на фронтальній проекції видима, бо вона знаходиться перед фронтальним слідом f° площини Q. На горизонтальній проекції видимою є частина прямої, що праворуч від точки М, бо вона розташована над горизонтальним слідом h° площини Q.

Якщо пряма розташована якось особливо, то таку обставину слід використовувати для спрощення побудови точки її перетину з площиною. Щоправда, особливе положення прямої може спричинити і значне ускладнення побудови точки перетину її з площиною (коли, наприклад, пряма профільна, а креслення задано на фронтальній і горизонтальній проекціях).

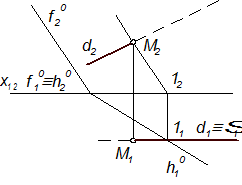Так, на рис. 4.22 показано побудову точки перетину фронтальної прямої d(d₁, d₂) з площиною D(f°, h°). У цьому разі доцільно через пряму провести фронтальну площину S(S₁), яка перетинає задану площину по її фронталі f(f₁, f₂): S∩hº = 1 (S₁∩hº₁ = 1₁), 1₂Îhº₂. 1₂Îf₂, f₂||f₂°. Точка М(М₁, М₂) перетину фронталі f з прямою d – це точка перетину прямої d з площиною D. Рис. 4.22

Дата добавления: 2014-01-14