Зоны Френеля

Принцип Гюйгенса-Френеля позволяет рассмотреть многие случаи дифракции света и часто дает результаты, вполне удовлетворительно согласующиеся с опытом.

Проиллюстрируем применение принципа Гюйгенса-Френеля на следующем примере. Пусть нам требуется определить амплитуду светового колебания, возбуждаемого в точке P сферической волной, распространяющейся в однородной изотропной среде (или другими словами, нас будет интересовать освещенность экрана в точке P, находящейся на оси симметрии).

На отверстии экрана “K” каждая точка этой сферической поверхности в соответствии с принципом Гюйгенса-Френеля будет являться источником вторичных когерентных волн (рис.12). Следовательно, интересующее нас световое возмущение в точке “P” заменяется световыми возмущениями, создаваемыми в этой точке элементами волнового фронта, называемыми зонами Френеля и построенными по особому правилу.

Итак, для учета интерференции вторичных волн Френель предложил разбить волновую поверхность падающей волны в месте расположения преграды на кольцевые зоны (зоны Френеля) по следующему правилу: расстояния от краев соседних зон до точки “P” должны отличаться на 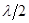, т.е.

, , ,…, .

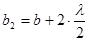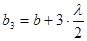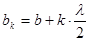Например: точк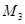и и 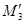находятся на расстоянии 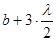от точки P.

Если теперь образующими М₁В и М₂В и т.д. описать конусы, то на сферической поверхности будем наблюдать шаровые пояса, которые и называются зонами Френеля. Зона вокруг вершины волнового фронта называется центральной зоной Френеля.

Зоны Френеля имеют следующие особенности:

1) При не слишком больших значениях k площади зон Френеля примерно одинаковы и равны площади центральной зоны.

,

где a – радиус волновой поверхности.

Если смотреть на волновую поверхность из точки P, то зоны Френеля будут выглядеть следующим образом (рис.13).

2) Зоны Френеля являются элементами волнового фронта, а т.к. разность хода лучей от 2 ^х соседних зон отличается на 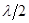, то эти лучи придут в точку P в противофазе и, следовательно, будут гасить друг друга, т.е. амплитуда результирующего колебания, вызванного совместным действием 2 ^х соседних зон будет равна разности амплитуд колебаний, возбуждаемых в точке B волнами, идущими от каждой зоны в отдельности.

Пусть a – амплитуда результирующих колебаний, возбуждаемых волнами, исходящими от всей поверхности (от всего волнового фронта);

a₀ – амплитуда колебаний, возбуждаемых в точке P действием центральной зоны;

a_i – амплитуда колебаний, возбуждаемых в точке P действием i-ой зоны.

Амплитуду результирующих колебаний можно представить в виде знакопеременного ряда:

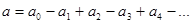
Вообще говоря, все эти амплитуды различны и образуют монотонно убывающую последовательность:

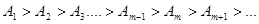
Здесь необходимо отметить, что зоны, достаточно далеко удаленные от центра O, посылают в точку B волны в противофазах практически с одинакового расстояния, вследствие чего их действие полностью уничтожается. Это дает основание утверждать, что для определения эффекта в точке B следует учитывать лишь действие центральных зон. При условии монотонного убывания амплитуд ряд этих чисел (A₁, A₂, A₃, …, A_m) представляет собой арифметическую прогрессию. В соответствии с этим для любых трех чисел 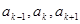справедливо соотношение: 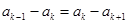или 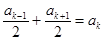. Теперь результирующую амплитуду “a” разобьем на части так, чтобы ее можно было представить в виде:

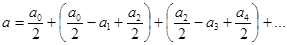
Из этого равенства видно, что в правой части уравнения в скобках уничтожаются все члены и остается .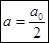

Таким образом, амплитуда, создаваемая в некоторой точке B всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной. Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке B будет равна a₀, т.е. в 2 раза превзойдет амплитуду, создаваемую в точке B всей сферической волновой поверхностью. Соответственно, интенсивность света в точке B в 4 раза будет больше, чем при отсутствии преград между источником света и точкой B на экране.

Рассмотрим теперь следующую ситуацию. Пусть часть волнового фронта перекрывается некоторым непрозрачным экраном, и пусть этот экран закрывает “k” зон Френеля (рис.14).

Тогда амплитуда результирующих колебаний:

или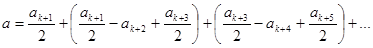

и следовательно 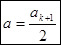. Видно, что амплитуда результирующих колебаний равна половине амплитуды колебаний световых волн, идущих от первой не перекрытой зоны Френеля.

Т.к. интенсивность световой волны I прямо пропорциональна 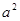(квадрату амплитуды), а амплитуда зависит обратно пропорционально от расстояния до источника, то , т.е. интенсивность световых лучей будет также уменьшаться с увеличением расстояния от источника до рассматриваемой точки. Отношение этих интенсивностей в случае с экраном и без него будет 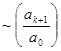, т.е. чем дальше экран, тем больше он охватывает зон Френеля и тем меньше будет интенсивность световых колебаний в точке B.

Итак, будет ли свет огибать препятствие или будет распространяться прямолинейно, зависит от соотношения между размерами экрана и зон Френеля. Если размеры экрана соизмеримы с шириной зон Френеля, т.е. если в пределах экрана укладывается небольшое число зон Френеля, то в точке B будет наблюдаться дифракционная картина.

Дата добавления: 2014-01-14