Дифракция Френеля от круглого отверстия

Зонная пластинка.

Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны Френеля, то интенсивность света в точке B резко возрастает. Такая пластинка, называемая зонной, действует подобно собирательной линзе, Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной пластинкой фазовая дает дополнительное увеличение амплитуды в 2 раза, а интенсивности света в 4 раза.

(Рекомендуется для самостоятельного изучения)

Различают два вида дифракции:

1) Если источник света S и точка наблюдения B расположены от препятствия настолько далеко, что лучи падающие на препятствие и лучи, идущие в точку B, образуют практически параллельные пучки, то говорят о дифракции в параллельных лучах или дифракции Фраунгофера. Дифракцию Фраунгофера[r] можно наблюдать, поместив за источником света S и перед точкой наблюдения B по линзе так, чтобы точки S и B оказались в фокальной плоскости соответствующей линзы.

2) В противном случае говорят о дифракции Френеля, которая наблюдается в сферических волнах.

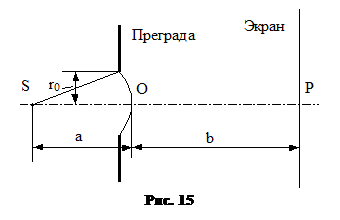Поставим на пути сферической волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса r₀ (рис.15). Расположим экран так, чтобы перпендикуляр, опущенный из источника света S, попадал в центр отверстия. На продолжении перпендикуляра возьмем точку P. При r₀<<a, b можно сказать, что

a=расстоянию от источника S до преграды;

b=расстоянию от преграды до точки P.

Можно легко получить, что

,

где m – целое число. Если a, b удовлетворяют этому соотношению, то отверстие оставит открытым ровно m зон Френеля, построенных для точки P. Отсюда .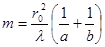

Амплитуда результирующих колебаний в точке P будет равна

.

Перед A_m берется знак «+», если m – нечетное,

«-», если m – четное.

Как и раньше, представим амплитуду результирующих колебаний в виде частичных сумм (для определенности положим A₁ºA₀):

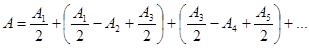
Положив выражения в скобках равными нулю, придем к формулам:

(m – нечетное)

(m – четное)

Амплитуды 2 ^х соседних зон практически одинаковы. Поэтому .

В результате получится:

«+», если m – нечетное, «-», если m – четное

Для малых значений m амплитуда A_m мало отличается от A₁. Следовательно, при нечетных m амплитуда колебаний в точке P будет»A₁, при четных m равна нулю.

Если удалить преграду, то амплитуда в точке P будет равна . Таким образом, преграда с отверстием не только не ослабляет освещенность в точке P, но, напротив, приводит к увеличению амплитуды почти в 2 раза, а интенсивности – почти в 4 раза.

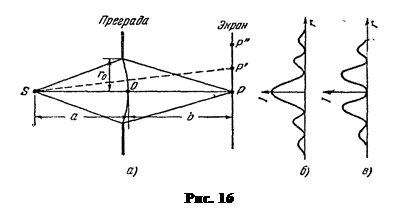
Выясним характер дифракционной картины, которая будет наблюдаться на экране, помещенном за преградой (рис.16).

Освещенность в разных точках экрана будет зависеть от расстояния r от точки P на оси x. В самой точке P интенсивность будет достигать максимума или минимума в зависимости от числа открытых зон Френеля. Пусть m=3, тогда в центре будет максимум (светлое пятно) /рис.17а/. Сместимся по экрану в точку P¢. Картина зон Френеля, видимая из точки P¢ изменится. Края отверстия закроют часть третьей зоны, одновременно частично откроется четвертая зона. В итоге интенсивность уменьшится и при некотором положении точки P достигнет минимума.

Если двигаться дальше в точку P¢¢, то действие открытых участков нечетных зон превысит действие открытых участков четных зон и интенсивность достигнет максимума, правда более слабого, чем максимум в точке P.

Таким образом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных концентрических колец. Ход интенсивности I с расстоянием r от центра картины изображен на рис.16(б) – m – нечетное, рис.16(в) – m – четное.

При перемещении экрана параллельно самому себе вдоль прямой SP будет происходить чередование дифракционных картин, соответствующих четному (нечетному) числу зон Френеля (расстояние b увеличивается, следовательно, значение m будет то четным, то нечетным).

Если отверстие открывает лишь часть центральной зоны Френеля, то на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает. Если отверстие открывает большое число зон Френеля, то чередование светлых и темных колей наблюдается лишь в очень узкой области на границе геометрической тени; внутри этой области освещенность оказывается практически постоянной.

Дата добавления: 2014-01-14