Дифракция Фраунгофера от щели

Пусть плоская волна падает перпендикулярно на экран со щелью шириной d (рис.18). Дифракционную картину будем наблюдать на экране в фокальной плоскости линзы. Т.к. в каждой точке фокальной плоскости линзы, например M, сходятся лучи, которые до линзы были параллельны между собой, то наблюдаемая здесь картина называется дифракцией в параллельных лучах.

Каждая точка щели будет являться источником вторичных волн. Из всех лучей, которые распространяются после щели, выберем только те, которые составляют угол j с первоначальным направлением, этот угол называется углом дифракции. На рисунке 18 - оптическая разность хода лучей. Разобьем участок BC на отрезки, равные 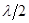и из этих точек проведем прямые параллельные AC до пересечения с AB. Таким образом, мы разобьем фронт волны в щели AB на такое же число отрезков по 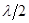, как и разность хода BC. Следовательно, щель AB мы разобьем на зоны Френеля, разность хода лучей от которых до точки M будет отличаться на .

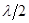Из геометрических построений получается 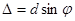. Число зон Френеля . Если z – четное число, то на отрезке AB укладывается четное число зон Френеля и свет от 2 ^х соседних зон приходит в точку M в противофазе и при наложении гасится. Следовательно, точка M освещена не будет. Если на отрезке AB укладывается нечетное число зон Френеля, то одна зона останется не погашена и точка M будет освещена.

Следовательно:

1) если 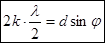- условие минимума освещенности при дифракции от одной щели;

2) если - условие максимума освещенности при дифракции от одной щели.

Итак, если оптическая разность хода лучей равна четному числу полуволн, то наблюдается минимум освещенности точки M при дифракции от одной щели. Если оптическая разность хода лучей равна нечетному числу полуволн, то наблюдается максимум освещенности точки M при дифракции от одной щели.

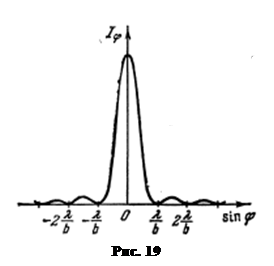
Рассмотрим, что будет представлять дифракционная картина в данном случае (рис.19). Расчеты показывают, что дифракционная картина будет симметрична относительно центра линзы.

,

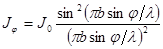где J₀ – интенсивность в центре дифракционной картины, b – ширина щели.

Напротив середины щели будет располагаться центральный или нулевой максимум, здесь будет наибольшая освещенность.

Боковые максимумы соответствуют уменьшению освещенности. Освещенность дифракционной картины убывает от центра к краям щели. Количество минимумов интенсивности определяется отношением ширины щели к длине волны l. Условие минимума , т.к. , то . Откуда . При ширине щели меньше l минимумы вообще не возникают, и интенсивность света монотонно убывает от середины щели к ее краям.

Краям центрального максимума соответствуют значения угла j, получающиеся из условия 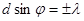. Эти значения равны 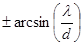. Поэтому угловая ширина центрально максимума равна 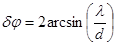. Когда d>>l, то 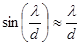и тогда формула для угловой ширины центрального максимума упрощается и имеет вид: .

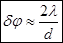Установим теперь качественный критерий, позволяющий определить, какой вид дифракции будет иметь место в каждом конкретном случае.

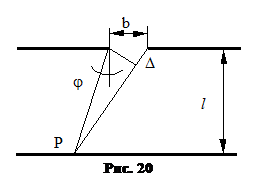
Найдем разность хода лучей от краев щели до некоторой точки P (рис.20).

Нас интересует случай, когда лучи, идущие от краев щели в точку P, почти параллельны. Следовательно: и 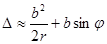. В пределе при r®¥ получаем . При конечном r характер дифракционной картины будет определяться соотношение между разностью хода (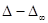) и длиной волны l.

Если , то дифракционная картина будет практически такой же, как и в случае дифракции Фраунгофера. При будет иметь место дифракция Френеля. Эти же условия можно записать в другом виде, введя безразмерный параметр 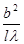. И тогда

Параметр 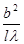непосредственно связан с числом открытых зон Френеля.

Если щель открывает малую долю центральной зоны Френеля (m<<1), то наблюдается дифракция Фраунгофера. Если открывает небольшое число зон Френеля (m~1), то на экране получается изображение щели, обрамленное по краям отчетливо видимыми светлыми и темными полосами. В случае, когда щель открывает большое число зон Френеля (m>>1) на экране получается равномерно освещенное изображение щели.

Итак, критерием применимости приближения геометрической оптики является не малость длины волны по сравнению с характерным размером преграды, а значение параметра 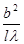(он должен быть >>1). Пусть, например, ; 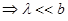, однако 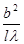@1, и поэтому на экране будет наблюдаться отчетливо выраженная Френелевская дифракция.

Дата добавления: 2014-01-14