Опыты Столетова[dd]. Законы фотоэффекта

Фотоэффект.

ОПРЕДЕЛЕНИЕ: Фотоэлектрическим эффектом или фотоэффектом называется испускание электронов вещества под действием света. Другое определение: фотоэффектом называется освобождение (полное или частичное) электронов от связей с атомами или молекулами вещества под действием света (видимого, ИК, УФ).

Если электроны выходят за пределы освещаемого вещества (полное освобождение), то эффект называется внешним. Открыт в 1887г. Герцем[ee], который обнаружил, что облучение искрового промежутка УФ-лучами значительно облегчает разряд. Подробно исследован Столетовым А.Г. в 1888г., который установил основные законы фотоэффекта.

Если же электроны теряют связь только со “своими” атомами и молекулами, но остаются внутри освещаемого вещества в качестве “свободных электронов” (частичное освобождение), увеличивая тем самым электропроводность вещества, то фотоэффект называется внутренним (открыт в 1873г. американским физиком У. Смитом).

Подробное исследование внешнего фотоэффекта было проведено А.Г. Столетовым (1839-1896) на установке, схематически показанной на рисунке 47, в результате чего были установлены следующие закономерности:

2. испускаемые под действием света заряды имеют знак минус («-»);

3. наибольшее действие оказывают УФ-лучи;

4. величина испущенного телом заряда пропорциональна поглощенной энергии.

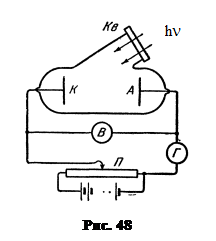Дальнейшие опыты Столетов проводил в вакууме на следующей установке (рис.48). Свет через кварцевое окно, прозрачное для видимого и УФ света, освещает катод из исследуемого материала. Электроны, испущенные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду. В результате в цепи течет ток, измеряемый гальванометром. Напряжение между электродами можно менять с помощью потенциометра.

С помощью такой установки были сняты вольтамперные характеристики. Если, не изменяя светового потока, увеличивать напряжение между катодом (К) и анодом (А), кривая зависимости тока (J) от напряжения (U) будет иметь вид (рис.49). Видно, что при некотором напряжении фототок достигает насыщения, т.е. все электроны, испущенные катодом, попадают на анод. Это значение напряжения называется напряжение насыщения, а достигнутое максимальное значение фототока – током насыщения.

Сила тока насыщения J_н определяется количеством электронов (е), испускаемых катодом за единицу времени под действием света.

Изменяя в этом опыте световой поток, удалось установить:

I закон фотоэффекта: при неизменном спектральном составе падающего на катод света сила тока насыщения (т.е. количество электронов, вырываемых светом с поверхности металла за 1сек) прямо пропорционально световому потоку.

Характерной особенностью рассматриваемого явления является то, что в цепи возникает ток, когда разность потенциалов между катодом (К) и анодом (А) равна нулю («0»). Это означает, что электроны, вылетевшие с катода, обладают такой энергией, что ее достаточно для совершения работы по преодолению сопротивления между катодом и анодом. Вместе с тем это означает, что свет является своеобразной фотоэлектродвижущей силой, поэтому по аналогии с гальванометрами и термоэлементами устройства, в которых ЭДС генерируется за счет света, называются фотоэлементами.

Для того чтобы фототок стал равным нулю, нужно приложить задерживающее напряжение U_з. (его также называют задерживающим потенциалом). При таком напряжении ни одному из электронов, даже обладающему при вылете с катода наибольшим значением скорости, не удается преодолеть задерживающее поле. Следовательно,

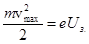
Если бы все фотоэлектроны имели бы одинаковую скорость “v”, то

· при условии 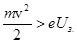все бы они достигали анода;

· при условии 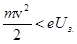все бы электроны задерживались полем и не доходили до анода;

· при условии 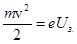фототок должен был бы прекращаться скачком.

Однако опыт показывает, что фототок плавно уменьшается по мере увеличения задерживающего поля. Следовательно, фотоэлектроны имеют различные скорости. На опыте было обнаружено, что U_з. не зависит от величины светового потока и для данного материала катода определяется частотой падающего на него излучения.

Отсюда:

II закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты падающего света и не зависит от его интенсивности.

Из экспериментальных данных было получено, что

,

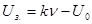где U₀ – зависит от свойств и материала катода; k=const.

Из данной формулы вытекает, что для того, чтобы электроны могли покинуть катод под действием света, необходимо выполнение условия: 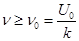или 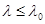. Частота n₀ называется красной границей фотоэффекта. Для разных материалов она различна (см. табл.), поэтому и не наблюдался для Zn-катода фотоэффект при его освещении белым светом, т.к. красная граница фотоэффекта для цинка лежит в УФ-области спектра.

Итак, если , то фотоэффекта нет;

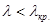, то фотоэффект есть;

III закон фотоэффекта: независимо от интенсивности падающего света фотоэффект начинается только при определенной (для данного металла) минимальной частоте света, называемой “красной границей” фотоэффекта.

Полученные экспериментальные результаты нельзя никак объяснить, оставаясь в рамках классической физики, на основе волновой теории. А именно:

1) Предположив, что электрон вылетает из металла под действием световой волны, нужно рассматривать ее как некоторую вынуждающую силу, амплитуда которой должна определять v_max вылетевших электронов. Следовательно, U_з. пропорциональна световому потоку и v_e должна увеличиваться с ростом интенсивности света, что противоречит II закону фотоэффекта.

2) Непонятна также зависимость U_з. от частоты падающего света. Согласно волновой теории свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла, иначе говоря, не должно было бы существовать “красной границей” фотоэффекта.

Эйнштейн показал, что все эти противоречия снимаются, если описанные явления рассматривать с позиций квантовой теории.

.432

7.2. Уравнение Эйнштейна для фотоэффекта.

В 1905г. Эйнштейн в экспериментальных законах фотоэффекта увидел убедительное доказательство идей Планка. Согласно Планку процессы испускания света происходят прерывисто, отдельными порциями. Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями с энергией . Однако Эйнштейн пошел значительно дольше. Он выдвинул гипотезу о том, что свет и распространяется в виде дискретных частиц (отдельных порций энергии), названных световыми квантами (или фотонами).

Эта гипотеза Эйнштейна была подтверждена рядом опытов. Наиболее непосредственное подтверждение дал опыт Боде. Тонкая металлическая фольга Ф (рис.50) помещалась между двумя газоразрядными счетчиками Сч. Фольга освещалась слабым пучком рентгеновских лучей, под действием которых она сама становилась источником рентгеновских лучей (это явление называется рентгеновской флуоресценцией). Вследствие малой интенсивности первичного пучка количество квантов, испускаемых фольгой, было невелико. При попадании в него рентгеновских лучей счетчик срабатывал и приводил в действие особый механизм М, делавший отметку на движущейся ленте Л. Если бы излучаемая энергия распространялась равномерно во все стороны, как это следует из волновых представлений, оба счетчика должны были бы срабатывать одновременно и отметки на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении.

Итак, было экспериментально доказано существование особых световых частиц – фотонов. Фотон обладает энергией 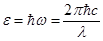, определяемой только его частотой w или длиной волны l. Подстановка значений и с приводит к формуле , где e выражена в электрон-вольтах, а l - в ангстремах. Длине волны l=0,555мк=5550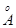соответствует энергия фотона e=2,23эВ. Для рентгеновских лучей (l»10^-4¸8×10²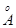) энергия фотонов лежит в пределах от 15эВ до ~100МэВ. Ниже в таблице приведены значения квантов энергии для некоторых длин волн, соответствующих различным видам электромагнитного излучения. Фотон не имеет массы покоя m₀, т.е. он не существует в состоянии покоя, а при рождении сразу приобретает массу и импульс . Из формул видно, что чем больше частота (n), тем больше энергия и импульс фотона и тем отчетливее выражены корпускулярные свойства света.

Объяснение фотоэффекта может быть сделано только на основе представлений о квантовой природе света.

Рассмотрим процесс поглощения фотона электроном металла. В результате поглощения фотона его энергия 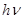целиком будет передана электрону. И запишем закон сохранения энергии для элементарного процесса, заключающегося во взаимодействии одного кванта света с веществом, сводящегося к передаче электрону дискретного количества энергии. При этом нужно учесть, что электрон в металле не является свободным и, чтобы покинуть тело металла, электрон должен преодолеть работу выход “A”. В этом случае уравнение, описывающее процесс поглощения одного кванта и возникновение электрона с наибольшей скоростью имеет вид:

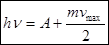- уравнение Эйнштейна для фотоэффекта.

Энергия, переданная фотоном электрону, идет на совершение работы выхода и сообщение электрону кинетической энергии.

Из уравнения Эйнштейна непосредственно видно, что скорость фотоэлектрона возрастает с ростом n и не зависит от его интенсивности (II закон фотоэффекта).

Согласно уравнению Эйнштейна существует частота n₀, при которой Е_к. фотоэлектрона равна нулю и фотоэффект прекратится (III закон фотоэффекта). Это будет, если или 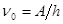. Видно, что “красная граница” зависит только от величины работы выхода (т.е. от материала фотокатода).

Учитывая, что 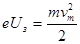, можно записать 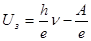. Это соотношение позволяет определить постоянную Планка из измерения наклона прямых, выражающих зависимость потенциала задержки от частоты падающего на фотокатод света (рис.51). Из опыта необ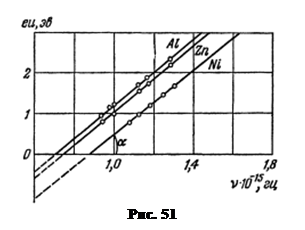ходимо определить величину напряжения, при котором исчезает фототок. Далее, необходимо построить графически зависимость eU_з. от n. Эта зависимость выражается прямыми, представленными на рисунке 51 для трех металлов: Al, Zn и Ni. Видно, что все прямые параллельны друг другу, причем наклон прямых не зависит от природы металла. По углу между прямыми и осью абсцисс можно определить постоянную Планка: , где k – соотношение размерных величин, принятых за единицы масштаба по осям eU и n.

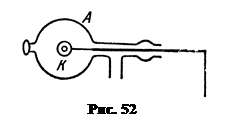Весьма точное определение “h” таким методом было выполнено П.И. Лукирским[ff] и С.С. Прилежаевым в 1930г. Для измерений использовали сферический конденсатор (рис.52), внутренний шарик которого был изготовлен из Ni и освещался светом ртутной лампы. Внешней обкладкой конденсатора являлся стеклянный шар, посеребренный изнутри, который играл роль анода «А». Спектральные линии ртути, возбуждавшие фотоэффект, выделялись монохроматором с кварцевой призмой. В этих опытах наблюдался относительно крутой спад кривых, характеризующих зависимость силы фототока от приложенного потенциала, т.к. в сферическом конденсаторе практически все фотоэлектроны достигают анода, что уменьшает ошибку в измерении U_з..

Отличное согласие результатов данных опытов с измерениями этой константы (h=6,62×10^-34Дж×с), проведенными совсем другими методами (законы абсолютно черного тела, коротковолновая граница сплошного рентгеновского спектра), являлось доказательством корректности квантового описания фотоэффекта.

И последнее: практическое использование фотоэффекта.

В современном эксперименте фотоэлектрические измерения световых потоков применяют во всем оптическом диапазоне. Измерения базируются на законах фотоэффекта, из которых в данном случае наиболее важна строгая пропорциональность силы тока насыщения и светового потока. Простейшим фотоэлектрическим приемником света является фотоэлемент (рекомендуется для самостоятельного изучения).

Дата добавления: 2014-01-14