Магнитный момент

Во внешнем магнитном поле на частицу с зарядом q действует сила Лоренца, которая определяется формулой

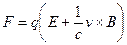. (2.21)

Из формулы (2.21) видно, что взаимодействие субатомной частицы с электромагнитным полем определяется её полным зарядом. К сожалению, полный заряд частицы в силу его квантованности даёт мало информации об её структуре. О последней можно судить по другим электромагнитным свойствам частицы и, в частности, по магнитному дипольному моменту.

Если электрический заряд размазан по частице, то он будет вращаться вместе с частицей, что приведёт к возникновению круговых токов, создающих магнитный дипольный момент m. Согласно классической электродинамике, замкнутый ток имеет следующую энергию взаимодействия:

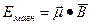, (2.22)

где 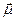- вектор магнитного дипольного момента. Величина его вычисляется по формуле m =1/с·(ток´площадь). Направление вектора 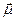перпендикулярно плоскости кругового тока. Связь между магнитным моментом и моментом количества движения можно установить, рассмотрев частицу с зарядом q, движущуюся со скоростью v по круговой орбите радиуса r. Частица обращается v/(2p r) раз в 1 сек, т.е.даёт ток qv/(2p r). Из определения m =1/с·(ток´площадь) следует, что

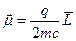. (2.23)

Результат этот страдает двумя недостатками. Он выведен на основе классической механики и электродинамики и представления о точечной частице, движущейся по круговой орбите. Вместе с тем в формуле (2.23) находят отражение два замечательных факта:

а) вектор m направлен по вектору орбитального момента количества движения L,

б) отношение m / L равно отношению q/2mc.

Таким образом, m и J связаны соотношением m = const· J.

В соответствии с (2.23) коэффициент пропорциональности должен иметь размерность e/mc, и поэтому его удобно записать в виде g( e/2mc ). Новая постоянная g является безразмерной; она характеризует величину отклонения значения реального магнитного момента от классического значения e/2mc. Теперь соотношение между m и J приобретает вид

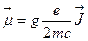. (2.24)

Помня, что 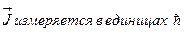, формулу (2.24) можно переписать в виде

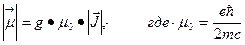. (2.25)

Постоянная m₀ называется магнетон, она представляет собой единицу измерения магнитных моментов субатомных частиц. Значение магнетона определяется массой частицы, используемой для его определения. В атомной физике, которая занимается решением задач, связанных с движением электронов, в выражении (2.25) используют массу электрона, и соответствующая единица магнитного момента называется магнетон Бора (m_В):

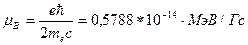. (2.26)

В субатомной физике магнитные моменты частиц выражаются в ядерных магнетонах. Ядерный магнетон получается из (2.26), если подставить вместо массы электрона массу протона.

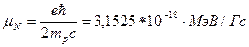. (2.27)

Таким образом, ядерный магнетон почти в 2000 раз меньше магнетона Бора.

В значении g -фактора заключена информация о структуре частицы. Для весьма многих состояний атомных ядер и для небольшого числа элементарных частиц g -факторы измерены. Объяснение экспериментально наблюдаемых значений g -факторов является важным делом теории.

Дата добавления: 2014-01-14