Полный момент количества движения

Спин

Спин -собственный момент количества движения частицы. Спин был первоначально введён для того, чтобы объяснить экспериментально наблюдаемый факт – расщепление спектральных линий на две близко расположенные компоненты. Между значением вектора спина 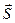и квантовым числом спина s имеется такое же соответствие, как между значением вектора орбитального момента и орбитальным квантовым числом l, а именно:

В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулём, спиновое квантовое число s может быть как целым (включая нуль), так и полуцелым (1/2, 3/2, 5/2,…), но при этом для каждой элементарной частицы он может принимать единственное присущее этому типу частиц значение. Так, спины p -мезона и К –мезона равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны ½. Спин фотона равен 1. Спин частицы невозможно изменить, так же как её заряд или массу. Это её неизменная квантовая характеристика

Как и в случае других квантовых векторов, проекция вектора спина s_z на любое фиксированное направление в пространстве (например, ось z) может принимать 2s+1 значение. Исключение составляют спины частиц с собственной массой, равной 0. В этом случае существует лишь две проекции спина на ось направления движения.

Максимальная величина квантового числа проекции спина s_z совпадает с ê S ê. Так как спин электрона равен ½, то проекция этого спина может принимать лишь два значения s_z =±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.

Если вероятности различных направлений спина одинаковы (спины частиц ориентированы произвольно), то говорят о равной нулю поляризации частиц. Если спины направлены в одну сторону, то говорят о единичной (или стопроцентной) поляризации. Если спин направлен перпендикулярно импульсу частицы, то говорят о поперечной поляризации. Продольная (круговая) поляризация означает, что спин частицы направлен вдоль её импульса.

В зависимости от того, как направлен спин относительно импульса при продольной поляризации, различают правую и левую поляризацию. Правополяризованной считается частица, спин которой направлен по импульсу, левополяризованной – против импульса. Для характеристики взаимного направления спина и импульса частицы используют понятие спиральности (см. рис. 2.2). Спиральностью h называют величину

. (2.18)

Правополяризованная частица имеет положительную спиральность (h =+1), левополяризованная –отрицательную (h = -1).

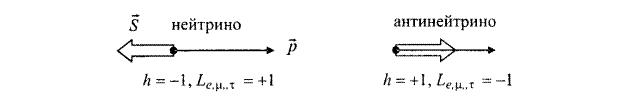
Рис. 2.2. Спиральности нейтрино и антинейтрино. Нейтрино –левополяризованная частица, антинейтрино –правополяризованная частица.

В классической физике полный момент количества движения частицы или системы частиц является непрерывной величиной. Полный момент количества движения (обычно обозначается 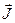) является вектором и должен быть задан тремя его проекциями J_x J_y J_z. Полный момент количества движения частицы складывается из его орбитального момента и собственного (спинового) момента :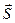

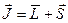. (2.19)

В квантовой теории ситуация аналогичная. Полный момент количества движения частицы также описывается соотношением (2.19), в котором векторные величины 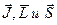заменены операторами полного момента 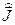, орбитального момента и спинового момента .

В отношении свойств вектора 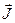в квантовой механике можно повторить те же утверждения, которые были сделаны ранее в отношении векторов и 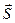. В соответствии с общими правилами для квантовых векторов проекция полного момента 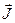на выделенную ось (z) может принимать 2 j +1 значение.

Чтобы получить вектор полного момента 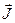, необходимо выполнить сложение векторов и 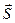. Такое сложение в квантовой физике отличается от классического, потому что квантовые вектора (соответствующие им квантовые числа l, s и j) не могут принимать непрерывный ряд значений, а всегда обязаны быть либо целочисленными, либо полуцелочисленными. Следствием этого является простое правило сложения квантовых векторов, иногда называемое правилом треугольника. Для случая (2.19) оно имеет вид:

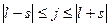. (2.20)

Левая часть этого неравенства соответствует минимальному значению вектора 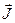, когда вектора и 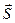направлены в противоположные стороны. Правая часть неравенства отвечает максимальному 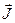, когда вектора и 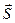сонаправлены. С учётом требований пространственного квантования все возможные j заключены в интервале от ½ l-s ½ до l+s и меняются в пределах этого интервала с единичным шагом (Dj=1). Что касается проекций на выделенную ось (z), то между ними существует простое алгебраическое соотношение j_z=l_z+s_z.

Из выше сказанного вытекает очевидное следствие: если спин частицы целый (или нуль), то полный момент j также целый (или нуль); если же спин полуцелый, то полный момент обязательно полуцелый.

Существует глубокая связь между спином и симметрией волновых функций, впервые указанная Паули и доказанная им с помощью релятивистской квантовой теории. Волновая функция системы n тождественных частиц с полуцелым спином, называемых фермионами, меняет знак, если переставить в ней любые две частицы. Волновая функция системы n тождественных частиц с целым спином, называемых бозонами, остаётся неизменной при перестановке в ней любых двух частиц.

Связь между спином и симметрией приводит к так называемому принципу Паули. Предположим, что две частицы обладают в точности одними и теми же квантовыми числами. Тогда говорят, что данные две частицы находятся в одном и том же состоянии. Перестановка 1«2 оставит волновую функцию двух частиц неизменной. Однако, если обе частицы являются фермионами, то волновая функция должна изменить знак и поэтому должна обратиться в нуль. Следовательно, можно говорить о принципе запрета, который гласит, что одно квантовомеханическое состояние может занять только один фермион.

Дата добавления: 2014-01-14