Атом водорода

Атом водорода – связанная система, состоящая из положительно заряженного ядра – протона– и отрицательного заряженного электрона. Размеры атома определяются размерами его электронной оболочки. Характерные размеры атомов »10^{-8 см. Потенциальная энергия связи электрона с протоном определяется кулоновским взаимодействием (протон предполагается покоящимся) и равна e 2}/r, где r расстояние между протоном и электроном. В этом случае уравнение Шрёдингера для стационарного состояния (волновая функция не зависит от времени) принимает вид:

. (2.11)

Возможные значения стационарных состояний электрона получаются при решении уравнения (2.11) с потенциалом U(r)=e²/r и определяются соотношением

(2.12)

где N –главное квантовое число, определяющее энергии различных состояний в атоме водорода (N =1,2,3…) см. рис. 2.1, а R – постоянная Ридберга (1,0974·10⁵ см^-1).

Волновая функция, описывающая стационарные состояния атома водорода, имеет стандартный вид

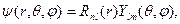(2.13)

где радиальная функция R_nl(r) и угловая функция Y_lm(q,j) удовлетворяют уравнениям

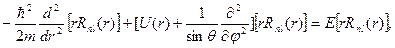(2.14)

(2.15)

Рис. 2.1. Орбиты модели атома Бора.

Состояния атома водорода описываются радиальным, орбитальным и магнитным квантовыми числами n, l, и m. Важно отметить, что между главным квантовым числом N, используемым в атомной спектроскопии, и квантовыми числами n и l существует следующая связь:

N=n+l. (2.16)

Квантовые числа n, l и m полностью характеризуют состояние электрона в атоме водорода в рассмотренной выше упрощенной модели. Состояние с N= 1 называется основным состоянием атома водорода, так как в этом состоянии обладает наименьшей энергией. Состояния с N= 2, 3, … называются возбуждёнными состояниями. Энергия возбуждения Е_возб (энергия, которую необходимо сообщить системе, чтобы она перешла из начального состояния N_i в конечное состояние N_f) определяется из соотношения

(2.17)

Все состояния от N= 1 до N= ¥ являются связанными состояниями, так как имеют отрицательные энергии. При приближении N к бесконечности энергии соседних состояний сближаются, и разница в энергиях этих состояний становится настолько мала, что расщеплённые уровни сливаются, и дискретный спектр уровней трансформируется в непрерывный (сплошной). Когда энергия электрона становится положительной (Е³0), система превращается в несвязанную, и электрон становится свободным.

Важной особенностью любой сферически симметричной системы является совпадение энергий состояний. Это явление носит название вырождения. В любом центральном потенциале энергия не зависит от числа m. Поскольку m= 0, ±1, ±2, ±3,…± l, то для каждого орбитального момента l имеется 2 l +1 значений m, и все эти значения отвечают одной и той же энергии. Таким образом, число различных (в данном случае по m) квантовых уровней с совпадающей энергией, т. е. кратность вырождения, также равно 2 l +1.Это минимально возможная кратность вырождения, присущая центральному полю. Обычно возникает дополнительное вырождение, обусловленное определёнными комбинациями n и l. Рассмотрим эту ситуацию для кулоновского потенциала.

В этом потенциале энергия определяется только главным квантовым числом N=n+l. Каждому уровню с главным кантовым числом N соответствует N состояний, различающихся квантовыми числами l= 0, 1, 2,…, N -1. Такое вырождение характерно только для кулоновского поля. Кроме того, каждое из этих вырожденных по l состояний (2 l +1)- кратно вырождено по числу m. Таким образом, полная кратность вырождения стационарного состояния с главным квантовым числом N даётся выражением

.

Дата добавления: 2014-01-14