Момент количества движения и спин частицы

Как известно из курса механики изотропность пространства приводит к выводу, что при движении замкнутой системы сохраняется векторная величина ,

которая называется моментом импульса.

В квантовой механике моменту импульса соответствует оператор

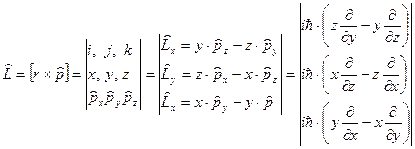, (2.8)

Можно показать, что любые две проекции оператора момента не коммутируют между собой

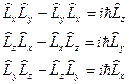. (2.9)

Поэтому не существует состояния, в котором бы все три и даже какие-либо две из трёх проекций момента импульса имели определённые значения. Отсюда следует, что не существует состояния, в котором и сам вектор момента импульса имел определённое значение, т. е. был бы полностью определён как по величине, так и по направлению. Иными словами, оператор момента не имеет собственных функций и соответствующих им векторных собственных значений.

Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление вектора момента по отношению к выделенному направлению (например, к внешнему магнитному полю) также квантуется (это называется пространственным квантованием). При этом проекция на это направление принимает дискретные значения L_z =, где m изменяется от + l до – l, т. е. имеет 2 l +1 значений.

(2.10)

Из изотропии пространства следует, что подобные соотношения возможны и для остальных выделенных направлений. В то же время не могут иметь в одном и том же состоянии определённые значения проекции углового момента вдоль двух различных направлений. Избранное направление можно поэтому взять произвольно. Такое направление обычно принимают за ось Z, так как в этом случае оператор в сферической системе координат выражается наиболее простой формулой.

Правило (2.10) по своей форме аналогично соответствующему правилу квантования момента импульса (1.9) в теории Бора. Однако между этими двумя правилами есть глубокое различие. В трактовке Бора под L понимается полный момент импульса частицы, тогда как в (2.10) речь идёт только об одной проекции момента импульса на какое-либо направление, а самого вектора импульса, как точно определённой величины вообще не существует.

Второй измеряемой величиной наряду с проекцией m_z на выделенную ось, характеризующей величину углового момента, является квадрат полного углового момента L². Но это не есть квадрат вектора L (которого не существует), а собственное значение квадрата оператора углового момента. Последний есть

.

Если Y есть собственная функция оператора квадрата углового момента, то собственное значение оператора квадрата углового момента может быть получено из решения уравнения .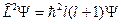

Дата добавления: 2014-01-14