Заряд ядра. Распределение заряда в ядре. Форм фактор

Все имеющиеся в настоящее время экспериментальные результаты согласуются с тем положением, что электрический заряд любой субатомной частицы Q всегда равен целому кратному элементарного кванта e:

Q=Ze, где e=4,8·10^-10 ед. СГСЭ или e=1,6·10^-19 Кº(4p·1,44 МэВ·Фм)^1/2

Квантование заряда было установлено в знаменитых экспериментах Милликена с масляными каплями.

Исторически самым первым методом, позволившим оценить заряд ядра и отождествить его величину (в зарядах протона) с атомным номером, является исследование углового распределения a -частиц при рассеянии их тонкими фольгами (опыты Герца и Мерсдена), которое описывается формулой Резерфорда

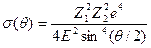, (3.2)

где Z₁ -атомный номер элемента, из которого изготовлена фольга; Z₂=2 атомный номер a -частицы; Е -энергия a-частицы; q-угол рассеяния a-частицы.

Более точно заряды ядер всех элементов Периодической системы были установлены по спектрам характеристического рентгеновского излучения, частота которого n_nm связана с атомным номером Z исследуемого образца законом Мозли

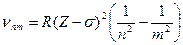, (3.3)

где R - постоянная Ридберга; s- постоянная экранирования; n,m – главные квантовые числа атомных электронных состояний, между которыми происходит радиационный переход.

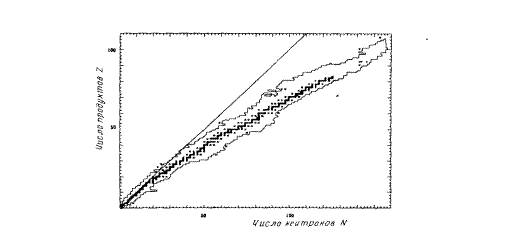
Рис. 3.1. Долгоживущие изотопы (линией ограничены ядра с измеренными временами жизни и массами).

Информацию о радиальном распределении плотности ядерного заряда можно получить, изучая рассеяние заряженных частиц. Особенно подходит для этой цели рассеяние высокоэнергетичных электронов, которые (в отличие от a -частиц) вступают только в электромагнитное взаимодействие с составляющими ядра. Это и позволяет прощупать распределение заряда. Для дифференциального сечения рассеяния электронов на ядре должна иметь место формула наподобие формулы Резерфорда. Однако эта формула должна отличаться от формулы Резерфорда в двух отношениях:

· должна быть применима к релятивистским частицам (v»c);

· должна учитывать наличие ненулевого (s=1/2) спина электрона.

Такая формула была получена Мотом в 1929 г. в рамках квантовой электродинамики и в пренебрежении отдачей ядра имеет вид

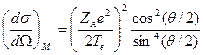. (3.4)

Формула Мотта получена в предположении бесструктурности (точечности) ядра. Если ядро -протяженный сферически-симметричный и бесспиновый объект с плотностью заряда r(r), то экспериментальное сечение упругого рассеяния электронов на нём будет отличаться от мотовского неким дополнительным множителем, который определяется только кулоновским взаимодействием и называется кулоновским форм-фактором:

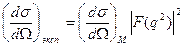. (3.5)

Величина форм-фактора F зависит от r(r) и может быть рассчитана для любого r(r), так как электроны не участвуют в ядерном (сильном) взаимодействии и взаимодействуют с ядром почти исключительно посредством электромагнитного поля.

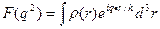, (3.6)

где q =( p - p ’) -переданный ядру импульс.

Кроме того, на современном уровне знаний электрон можно считать точечной частицей. Таким образом, в форм-фактор упругого рассеяния дает вклад только r(r) ядра. Схема нахождения r(r) такова. Определяют 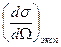и затем сравнивают с 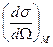. Из их сравнения находят F (q²).

Эксперименты по неупругому рассеянию электронов показали, что протон и нейтрон не являются точечными частицами. Для протона распределение электрического заряда имеет вид:

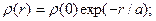
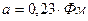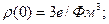. (3.7)

Из (3.6) можно найти среднеквадратичный радиус протона, учитывая, что заряд, сосредоточенный в шаровом слое единичной толщины, равен 4pr²r(r):

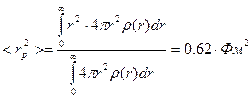. (3.8)

Отсюда размер протона 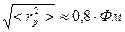. Размер нейтрона примерно такой же.

Для ядер, расположенных вблизи долины стабильности, были установлены следующие закономерности.

• Пространственное распределение протонов и нейтронов для ядер вблизи долины стабильности практически совпадают.

• Плотность ядерной материи в центре ядра r ₀ приблизительно одинакова и составляет ~17нукл./Фм³.

• Толщина поверхностного слоя t (спад плотности от 0,9 до 0,1 r ₀) у всех ядер приблизительно одинакова t =4,4 a =2,4Фм

Дата добавления: 2014-01-14