A. Методы ядерных сил

Геометрические размеры ядра.

В понятие размера ядра следует включить не только геометрическую протяженность, так как современное знание о ядре позволяет говорить, что существенными характеристиками ядер являются их масса, заряд, спин и магнитный момент. Так, например, заряд (подобно составляющим его нуклонам) распределен в ядре непрерывно от центра ядра к его периферии, которая может быть определена как область, где плотность заряда приближается к нулю. Поэтому следует говорить о ядерной плотности и распределении её по объему ядра, а не просто о величине и размерах идеализированного шара. Кроме того, следует заметить, что вообще у нас нет оснований считать ядра сферически симметричными объектами, хотя известно, что многие ядра обладают такой симметрией.

Из этих замечаний видно, что определение ядерных «размеров» является весьма серьезной задачей. Последние (согласно Хофштадтеру) можно разделить на три группы:

a. методы ядерных сил:

a. рассеяние a-частиц, протонов, нейтронов и быстрых ионов,

b. a-радиоактивность,

c. дифракционные явления при высоких энергиях.

b. электрические и магнитные методы:

a. рассеяние электронов,

b. изотопический сдвиг и зеркальные ядра,

c. m-мезоатомы,

d. тонкая структура рентгеновских спектров,

c. комбинированные методы:

a. полуэмпирическая формула Вейцзекера,

b. фоторождение p⁰-мезонов.

Рассеяние a-частиц, протонов, нейтронов и быстрых ионов. Рассеяние a-частиц был первым методом, позволившим оценить размер ядра. В современном виде это метод рассеяния не только a-частиц, но и протонов, нейтронов и быстрых ионов. Для интерпретации результатов экспериментов по рассеянию используется оптическая модель ядра, в которой рассматривается движение рассеиваемой частицы в потенциальном поле ядра, описываемом комплексным потенциалом, мнимая часть которого обеспечивает процесс поглощения налетающих частиц. Для обеих частей оптического потенциала -действительной и мнимой- можно принять один и тот же вид кривой потенциальной энергии. Типичная форма этой кривой дается выражением

(3.9)

где V и W -амплитуды вещественной и мнимой частей потенциала, Z -атомный номер налетающего ядра (частицы), j(r)- потенциал кулоновского поля ядра, рассматриваемого как равномерно заряженный шар, R -эффективный радиус действия ядерных сил (искомый радиус ядра), а -размытость ядерной части потенциала (a =0,5·10^{-13 см).}

Значение максимально-правдоподобных значений параметров оптического потенциала получают в ходе описания экспериментальных данных по рассеянию теоретической кривой. Результаты такого анализа экспериментов по рассеянию a -частиц на ядрах в широком диапазоне A и Z от ¹²C до ¹⁸¹Ta показали наилучшее описание всего массива данных при R=r₀·A^1/3, где r₀=1,35·10^{-13 см.}

Альфа-радиоактивность. Метод определения радиуса a-радиоактивных ядер основан на том, что выражение для. среднего времени жизни a-радиоактивных ядер t содержит радиус ядра R

, (3.10)

т.е. измерения времени жизни a-радиоактивных ядер позволяют получить информацию о радиусах ядер. Анализ обширного экспериментального материала о времени жизни a-радиоактивных ядер дает значения радиусов таких ядер порядка

R=r₀ ×A^1/3, где r₀ = 1,4×10^-13см.

b Электрические и магнитные методы. Одним из главных электромагнитных методов является рассеяние быстрых электронов на ядрах. Изучение структуры ядра с помощью рассеяния на нем электронов началось с пионерских работ Хофштадтера[1] и его сотрудников. Схема, использованной ими установки изображена на рис. 3.2. Электронный ускоритель дает интенсивный пучок электронов с энергией от 250 МэВ до нескольких ГэВ. Электроны пучка транспортируются в мишенную камеру, где рассеиваются на соответствующей мишени. Интенсивность пика упруго рассеянных электронов определяется как функция угла рассеяния.

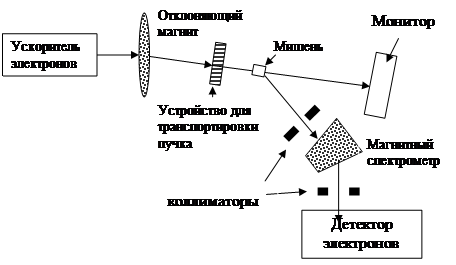Рис. 3.2. Схема установки для изучения упругого рассеяния электронов.

Наиболее грубо распределение заряда в ядре описывает однопараметрическая функция, например соответствующая однородному гауссовому распределению. Такие распределения приводят, однако, к плохому совпадению с экспериментальными данными, и поэтому простейшим приемлемым приближением считается двухпараметрическое распределение Ферми:

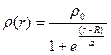, (3.11)

где r₀ – нормировочная постоянная, а и с –параметры, описывающие структуру ядра. Распределение Ферми показано на рис. 3.2. Параметр R называется радиусом полуплотности, а (t=(4ln3)а»4.4а) – толщиной поверхности ядра.

Результаты многочисленных экспериментов можно систематизировать следующим образом:

1) для средних по весу и тяжелых ядер среднеквадратичный радиус распределения заряда можно с хорошим приближением представить формулой

[ <r²> ]^1/2 =r₀× A^1/3, r₀=0,94· 10^-13см; (3.12)

2) радиус полуплотности (обычно ассоциируется с радиусом ядра) и толщина поверхности ядра приближенно даются формулами

c(Фм)=R=1,18 A^1/3-0,48 t»2,4(Фм); (3.13)

3) истинное распределение электрического заряда в ядре более сложное, чем описываемое двухпараметрическим распределением Ферми. В частности, плотность внутри ядра не является постоянной, как это предполагается в распределении (3.11). Она может и возрастать, и убывать по направлению к центру. Два таких случая показаны на рис. 3.2.

Рис. 3.2. Распределение нуклонов для ядер ⁴⁰Ca и ²⁰⁸Pb, полученное из экспериментов по рассеянию электронов.

Мю-мезоатомы. Метод основан на явлении образования неустойчивых мезоатомов при приближении m-мезона к атомному ядру. Измерение энергии g- или рентгеновских квантов позволяет приближенно определить размеры ядра.

3.3.3. Масса ядра.

Масса ядра- одна из важнейших характеристик. Массу отдельных изотопов можно определить двумя способами. Первый основан на том, что массу отдельного ядра можно непосредственно измерить в масс-спектрометре, устройство которого схематически представлено на рис. 3.3. В масс-спектрометре частица проходит через специальным образом расположенные электрические и магнитные поля. Попадающие в прибор частицы фокусируются на фотопластинку. Поля в приборе подобраны таким образом, что место попадания частицы на фотопластинку не зависит от скорости частицы и определяется только их массой.

Второй метод определения массы атомов состоит в использовании энергетического баланса специально подобранной реакции, что позволяет косвенно определить массы. Рассмотрим этот метод подробнее. С этой целью запишем реакции, в которой частица a сталкивается с ядром A, в результате чего возникают ядро B и частица b:

A + a ® B + b + Q, (3.14)

где Q-высвобождаемая энергия, т.е. избыток кинетической энергии конечных продуктов. Значение Q точно равно разности масс правой и левой частей приведенного выше уравнения.

Q/c²= (M_A + m _a) – (M_{B +} m_b). (3.15)

Рис. 3.3. Схема масс-спектрометра. 1-магнитное поле;

2- фотопластинка;

3-электрическое поле.

Из уравнения (3.15) видно, что по энергии ядерной реакции можно установить массу одного из продуктов, если известны массы остальных. В качестве единицы измерения используется углеродная единиц, атомная единица массы (а.е.м.), численно равная массе 1/12 массы нуклида ¹²С. Массовую единицу u можно выразить в единицах МэВ и г:

1 u = 931,484 МэВ = 1,66043·10^-24г.

Для сравнения, массы свободных нуклонов равны

m_p = 938,3 МэВ/c²,

m_n = 939,6 МэВ/c².

Масса ядра, состоящего из Z протонов и N нейтронов, определяется выражением

m(Z,N)=Zm_p + Nm_n –W/c², (3.16)

где W -энергия связи, т.е. энергия, которую необходимо затратить, чтобы разделить ядро на отдельные нуклоны и разнести их на бесконечно большие расстояния друг от друга, m_p, m_n -масса протона и нейтрона, соответственно. Здесь пренебрегают малым добавком к массе ядра, обусловленным эффектами связывания электронов в атоме.

В таблицах масс приводятся не массы ядер, а массы нуклидов (атомов). При вычислении энергетических характеристик распадов и ядерных реакций имеют дело с разностями масс, поэтому масс электронов, входящих в состав нуклидов, сокращаются. Таким образом, с точностью до разности энергий связи электронов в нуклидах такая замена приемлема.

Полезным понятием в ядерной физике является дефект массы ядра, связанный с его энергией связи. Дефектом массы ядра называется разность между массой рассматриваемого ядра, выраженного в атомных единицах массы, и соответствующим массовым числом А:

D(Z, A) = М_яд(Z, A)- А

Дата добавления: 2014-01-14