III. Агрегатный индекс как исходная форма индекса

Общий индекс, полученный путем сопоставления итогов, выражающих величину сложного явления в отчетном и базисном периодах при помощи соизмерителей, называется агрегатным индексом. Способ исчисления общего индекса таким путем называется агрегатным способом.

Агрегатный индекс - основная форма всякого экономического индекса. Он представляет собой отношение сумм произведений индексируемых величин и их весов.

1) Агрегатный индекс физического объема:

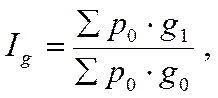
где ро - цена базисного периода, принимаемая в качестве сопоставимой для двух периодов.

2) Агрегатный индекс цен:

Если исчислим индекс цен по количествам отчетного периода, тогда формула агрегатного индекса цен будет следующая:

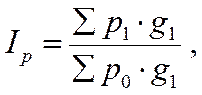
где ро и р1 - цены на продукты соответственно в отчетном и базисном периодах;

q1 - количество продукции отчетного периода.

В числителе - сумма фактического товаро-оборота отчетного периода. В знаменателе - товарооборот отчетного периода в базисных ценах.

3) Агрегатный индекс себестоимости:

Характеризует среднее изменение себестоимости продукции отчетного периода по одноименному (сопоставимому) с базисным периодом кругу продукции. Числитель индекса характеризует затраты на производство в отчетном периоде сопоставимой продукции, знаменатель - те же затраты на производство, которые были бы, если бы себестоимость оставалась на уровне базисного периода.

4) Агрегатный индекс производительности труда:

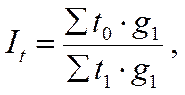
где t - затраты труда на единицу продукции.

Числитель характеризует количество труда, которое нужно было бы затратить на производство продукции отчетного периода при уровне производительности труда базисного периода. Знаменатель этого индекса - фактические затраты труда в отчетном периоде на производство продукции.

Пример 4. Товарооборот торгового объединения по продаже молока и яиц в марте по сравнению с февралем возрос с 1760 до 2300 рублей. Данные о выручке, количестве и цене проданных товаров следующие:

Продукты	Товарооборот	Количество	Цены за Единицу
февраль	март	февраль	март	февраль	март
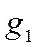
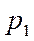
Молоко Яйца (дес.)					0,35 1,20	0,30 1,00
Итого	1760	2300

Как же повлияло на рост товарооборота изменение цен и количество проданных товаров?

1) Рассчитываем индекс товарооборота:

или 130,7 %,

где 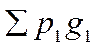- сумма фактического товарооборота отчетного периода;

- сумма фактического товарооборота за базисный период.

2) Индекс физического объема товарооборота:

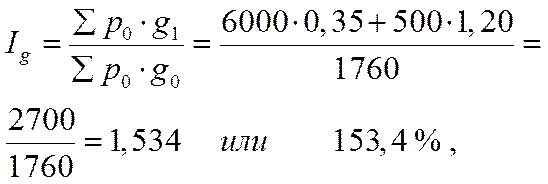
- сумма товарооборота отчетного периода в базисных ценах.

3) Индекс цен:

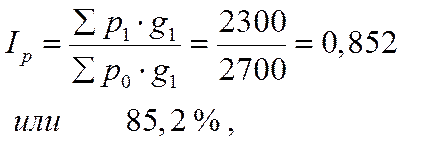
Исчисленные данные показывают, что на общее изменение товарооборота, составившее 30,7%, количество проданных товаров повлияло в сторону увеличения на 53,4%, зато цены - в сторону снижения на 14,8% (100% - 85,2%).

В индексе физического объема товарооборота цены являются весами и они берутся неизменными в отчетном и базисном периоде.

В индексе цен количества товаров выступают как веса индекса, и эти количества берутся одни и те же для отчетного и базисного периода, чтобы индекс показал только изменение уровней цен.

Индекс физического объема товарооборота (Iq) показывает, что объем продажи товаров вырос в отчетном периоде на 53,4%. Разность между числителем и знаменателем индексного отношения характеризует прирост товарооборота в неизменных ценах в отчетном периоде: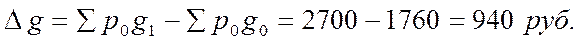

Индекс цен (Ip) показывает снижение цен на 14,8%. Он характеризует то, как изменился уровень цен на товарную массу, которую население купило в отчетном периоде.

Экономия населения от снижения цен в отчетном периоде на товары составила 400 руб.:

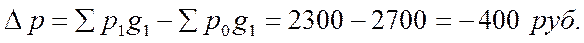
Общий итог влияния двух факторов на рост товарооборота равен:

Индексы с постоянными и переменными весами

Если расчет агрегатных индексов физического объема продукции и товарооборота производится по неизменным ценам базисного периода, это позволяет, используя индексный ряд за несколько периодов, получить динамику стоимости продукции и динамику товарооборота в неизменных (сопоставимых) ценах, т.е. в ценах какого-то одного прошлого периода. Такие индексные ряды называются индексами с постоянными весами.

Для индексов с постоянными весами действует правило: произведение цепных индексов равно базисному индексу.

Пример 5. Имеются следующие данные об объеме производства и стоимости продукции:

Продукция	Произведено продукции за I кв.	Цена 2001г	Стоимость продукции в неизменных ценах 2001 года, тыс.руб.
Продукция А, тыс.т. Продукция Б, млн.шт.	5,5	6,2	7,0
Итого

Требуется рассчитать индексы себестоимости с постоянными весами.

Базисные индексы:

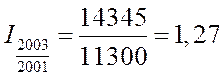
Цепные индексы:

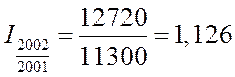
Взаимосвязь базисных и цепных индексов:

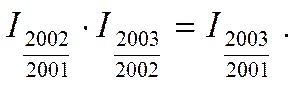
1,126 ·1,128 = 1,27.

Несколько иное положение с индексами цен, себестоимости и производительности труда. Если в качестве весов принимается количество продукции отчетного периода (q1), эти индексы образуют индексные ряды с переменными весами, поскольку в каждом отдельном индексе отчетный период изменяется.

Пример 6. Имеется следующая информация о продаже и ценах овощной продукции:

Товар	Среднедневная продажа, кГ	Цена за 1 кГ., руб.
октябрь	ноябрь	декабрь	октябрь	ноябрь	декабрь
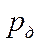
Овощи Фрукты				1,2 1,0	1,0 1,8	2,2 2,5

Требуется рассчитать индексы цен с переменными весами.

Для изучения изменения цен по месяцам IV квартала определяются цепные и базисные общие индексы цен.

1. Среднее изменение цен в ноябре по сравнению с октябрем:

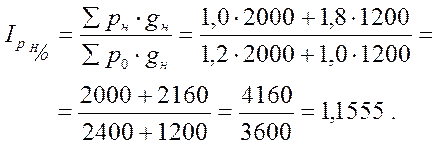
2. Среднее изменение цен в декабре по сравнению с ноябрем:

3. Среднее изменение цен в декабре по сравнению с октябрем:

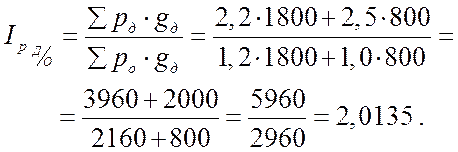
Дата добавления: 2014-01-14