Условный экстремум функции нескольких переменных

Определение 18.1. Градиентом функции в точке называется п – мерный вектор, т.е. упорядоченный набор из п действительных чисел, определяемой формулой

.

Под классической задачей на условный экстремум будем понимать экстремальную задачу вида

, ,

с ограничением D как множеством решений некоторой системы уравнений.

Определение 18.2. Пусть функции 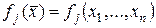, заданы на множестве 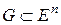. Классической задачей на условный экстремум называется следующая экстремальная задача:

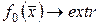, (18.1)

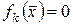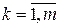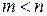, , . (18.2)

Каждое решение системы уравнений (18.2) есть точка множества G. Совокупность всех таких точек представляет собой ограничение . Если уравнения (18.2) можно разрешить относительно т каких-либо переменных, то, подставив их значения вместо соответствующих аргументов функции 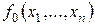, сведем задачу (18.1), (18.2) на условный экстремум к задаче на безусловный экстремум функции переменных. Другой подход к решению задачи (18.1), (18.2) (метод Лагранжа) состоит к сведению этой задачи к экстремальной задаче без ограничений для функции Лагранжа переменных. При этом будем предполагать, что векторы , 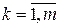в точке 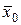условного экстремума линейно независимы. Указанное ограничение на векторы носит название условия регулярности в точке .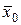

Определение 18.3. Функцией Лагранжа для экстремальной задачи (18.1), (18.2) называется функция переменных, определяемая формулой

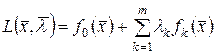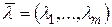, . (18.3)

Переменные 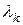, 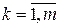называются множителями Лагранжа.

Теорема 18.1. (Необходимое условие локального условного экстремума). Если 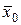- точка условного локального экстремума в задаче (18.1), (18.2) и в окрестности этой точки функции 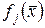, непрерывно дифференцируемы, то найдутся множители Лагранжа 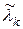, , 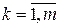одновременно не равные нулю, такие, что выполняются условия

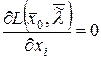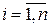, . (18.4)

Итак, при условиях теоремы 18.1 локальное решение задачи (18.1), (18.2) находится среди решений 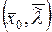следующей системы с неизвестными

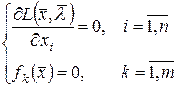. (18.5)

В симметричной форме систему (18.5) можно переписать так

.

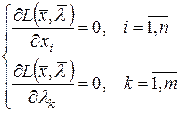Если 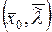- решение системы (18.5), то 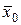не обязательно является точкой условного локального экстремума в задаче (18.1), (18.2). Дополнительное исследование указанного решения на экстремум определяется с помощью следующего достаточного условия.

Теорема 18.2. (Достаточное условие локального условного экстремума). Если 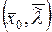- решение системы (18.5) и функции 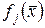, дважды дифференцируемы в точке 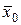, причем

(18.6)

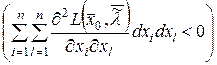, (18.7)

при условии, что приращения , 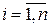удовлетворяют дополнительным соотношениям

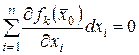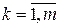, , (18.8)

то 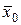- точка локального условного минимума (максимума).

Заметим, что в случае задачи

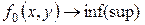, (18.9)

(18.10)

на локальный условный экстремум для функции двух переменных условия (18.6), (или (18.7)) и (18.8) равносильны условию

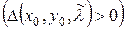, (18.11)

где

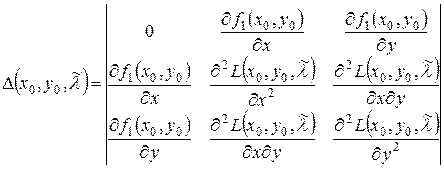. (18.12)

Теорема 18.3. Если функция Лагранжа (18.3) в задаче (18.1), (18.2) выпуклая (вогнутая) на выпуклом открытом множестве G, то любая точка 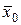локального условного минимума (максимума) в задаче (18.1), (18.2) является и точкой ее глобального условного минимума (максимума).

Достаточными условиями выпуклости (вогнутости) функции Лагранжа являются условия вида (18.6) ((18.7)) и (18.8) для всех точек 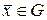и любых . В случае задачи (18.9), (18.10) указанные условия равносильны условию , где определяется формулой (18.12).

Пример. Среди всех прямоугольников данного периметра 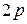найти прямоугольник наибольшей площади.

Решение. Обозначим стороны прямоугольника через х и y. Периметр такого прямоугольника равен 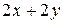, а площадь - 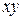. Таким образом, решение поставленной задачи сводится к нахождению глобального условного максимума в задаче

. (18.13)

Найдем точку локального условного максимума в задаче (18.13), для чего составим функцию Лагранжа

.

Имеем

, .

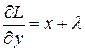Точка локального условного максимума находится среди решений системы

.

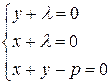Указанная система имеет единственное решение 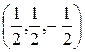. Применим к этому решению условие (18.11). Предварительно находим

, , , .

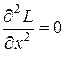По формуле (18.12) для любых х, y, 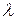получаем

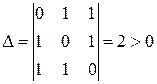. (18.14)

Отсюда следует, что точка 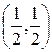является точкой локального условного максимума в задаче (18.13). Так как вследствие (18.14) функция 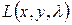вогнутая, то указанная точка есть и точка глобального условного максимума в задаче (18.13). Итак, искомый прямоугольник является квадратом со стороной .

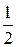Из неклассических задач на условный экстремум сформулируем лишь задачи математического и выпуклого программирования.

Определение 18.4. Пусть функции 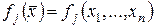, заданы на множестве 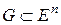. Задачей математического программирования для функции 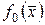называется следующая экстремальная задача

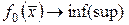(18.15)

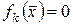, (18.16)

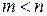, , . (18.17)

Здесь ограничение является множеством решений системы уравнений (18.16) и неравенств (18.17).

Определение 18.5. Экстремальная задача (18.15) – (18.17) на условный минимум называется задачей выпуклого программирования, если

1) G – выпуклое множество;

2) 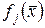, выпуклые функции на G;

3) неравенства (18.17) линейные.

На практике для приближенного поиска экстремума, как правило, используются численные методы. Среди них наиболее широко применяется градиентный метод. В общих чертах этот метод состоит в построении специальной последовательности точек, сходящейся к точке экстремума. При этом отрезок, соединяющий две соседние точки указанной последовательности, направлен по градиенту функции в предыдущей точке. Описание численных методов поиска экстремума можно найти, например, в [3] и [4].

Дата добавления: 2014-01-14