Безусловный экстремум функции нескольких переменных

Результаты, приводимые далее, подобны результатам из п. 15, 16 для функции одной переменной.

Теорема 17.1. Если - точка безусловного локального экстремума функции и в этой точке существует какая-либо частная производная , , 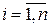то эта частная производная равна нулю.

Доказательство. Рассмотрим функцию 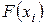одной переменной 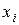, определенную формулой

.

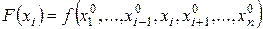Эта функция дифференцируема в точке 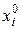, ибо по определению частной производной имеем

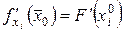. (17.1)

Далее, из определений локального экстремума функции одной и нескольких переменных следует, что если 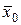- точка локального безусловного экстремума функции 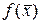, то 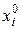- точка локального экстремума функции 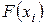. Поскольку 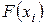дифференцируема в точке 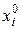, то на основании необходимого условия локального экстремума функции одной переменной производная 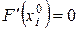. Отсюда в силу (17.1) следует утверждение теоремы.

Заметим, что для дифференцируемой в точке 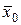функции 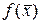по определению дифференциала, из условия следует выполнение системы равенств 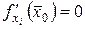, 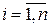. Обратное утверждение в общем случае не имеет места.

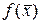Определение 17.1. Всякое решение уравнения для функции , заданной на открытом множестве 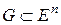, называется стационарной точкой для этой функции.

Не каждая стационарная точка функции 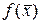является точкой безусловного локального экстремума этой функции. Поэтому стационарные точки подлежат дополнительному исследованию с помощью достаточных условий.

Теорема 17.2. (Достаточные условия безусловного локального экстремума). Если функция 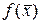определена на открытом множестве 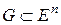и дважды дифференцируема в точке , причем

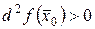
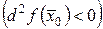, , (17.2)

то 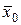- точка безусловного локального минимума (максимума) этой функции.

Доказательство теоремы 17.2 можно найти в [1].

Условие 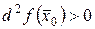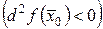можно проверить с помощью критерия Сильвестра (см. § 8).

Сформулируем теперь достаточные условия безусловного глобального экстремума функции нескольких переменных.

Теорема 17.3. Если функция 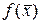выпуклая (вогнутая) на открытом выпуклом множестве 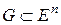, то любая точка безусловного локального минимума (максимума) этой функции является и точкой ее безусловного глобального минимума (максимума).

Теорема 17.4. Если функция 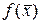выпуклая (вогнутая) на открытом выпуклом множестве 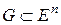и дифференцируема в точке , причем , то 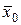является точкой безусловного глобального минимума (максимума) этой функции на G.

Пример. Исследовать на безусловный глобальный экстремум функцию

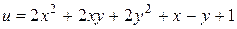(17.3)

на всем пространстве .

Решение. По определению дифференциала

.

В нашем случае уравнение 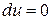имеет вид

.

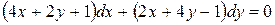Отсюда в силу произвольности и 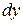получаем систему уравнений

,

которая имеет одно решение 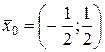. Функция (17.3) дважды дифференцируема в , причем

, , .

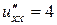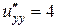Покажем, что 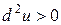во всех точках 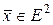. Для этого воспользуемся критерием Сильвестра (см. § 8):

, .

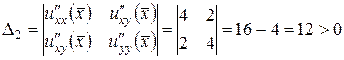Отсюда согласно теореме 14.2 функция (17.3) выпуклая во всем пространстве . Следовательно, на основании теоремы 17.4 точка 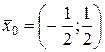является точкой безусловного глобального минимума функции (17.3).

Исследование задач на безусловный глобальный экстремум для функции , заданной на замкнутом множестве, опирается на теорему Вейерштрасса, согласно которой всякая непрерывная на замкнутом множестве функция 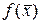имеет на этом множестве точки глобального минимума и максимума. При этом глобальный экстремум может достигаться либо во внутренней точке множества, либо на его границе.

Дата добавления: 2014-01-14