Глобальный экстремум функции одной переменной

Как уже отмечалось, не каждая точка локального минимума (максимума) функции одной переменной есть точка глобального минимума (максимума) этой функции. Как явствует из следующей теоремы, для выпуклой (вогнутой) функции всякая ее точка локального минимума (максимума) является и точкой глобального минимума (максимума).

Теорема 16.1. Если функция 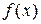выпуклая (вогнутая) на интервале 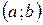, то любая точка ее локального минимума (максимума) является и точкой глобального минимума (максимума) на .

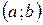Доказательство. Пусть функция 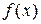выпуклая на интервале 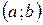и точка 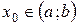есть точка локального минимума этой функции. По определению точки локального минимума существует 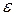- окрестность точки 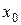такая, что

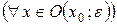
. (16.1)

Обозначим через 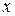произвольную точку интервала 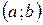, отличную от 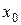. Пусть t – любое действительное число, удовлетворяющее условию

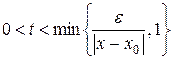. (16.2)

Покажем, что точка 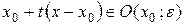. Действительно, учитывая (16.2), получим

,

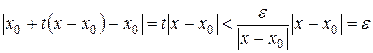т.е. 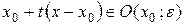. Далее, так как 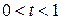, то в силу выпуклости функции 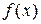и условия (16.1), находим

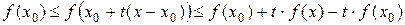
или

,

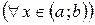
т.е. точка 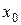- точка глобального минимума.

Пусть теперь функция 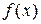вогнутая на интервале 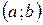и 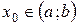- точка локального максимума этой функции. Тогда в силу сделанных ранее замечаний функция 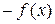выпуклая на интервале 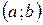и 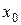- точка локального минимума. Отсюда по доказанному выше 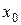- точка глобального минимума функции 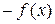или все равно что 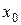- точка глобального максимума функции 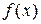на интервале .

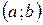Теорема 16.2. Если функция 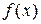выпуклая (вогнутая) на интервале 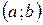и дифференцируема в точке 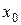, причем 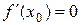, то 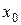является точкой глобального минимума (максимума) этой функции на интервале .

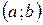Доказательство. Пусть функция 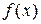выпуклая на интервале 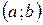, дифференцируема в точке 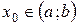, причем

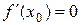. (16.3)

Тогда по определению выпуклой функции выполняется неравенство

для всех 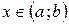и 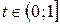. Отсюда

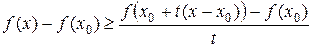. (16.4)

В силу дифференцируемости функции 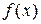в точке 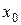справедлива следующая формула Тейлора с остаточным членом в форме Пеано

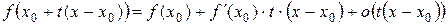, (16.5)

где 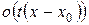- бесконечно малая при 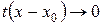более высокого порядка, чем 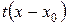, т.е.

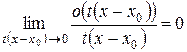. (16.6)

В предположении 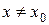, условие 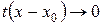равносильно условию 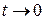. Следовательно, на основании (16.6)

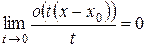. (16.7)

В силу (16.5) неравенство (16.4) может быть переписано в виде

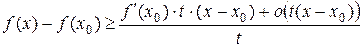
или вследствие (16.3) в виде

.

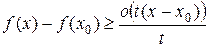Отсюда по свойству предела функции в силу (16.7) получаем

.

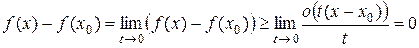Таким образом,

,

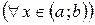
т.е. 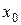- точка глобального минимума функции на интервале .

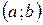Пусть теперь функция 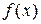вогнутая на интервале 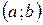, дифференцируема в точке 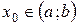, причем 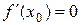. Тогда функция 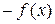выпуклая на интервале 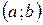, дифференцируема в точке 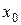и ее производная в этой точке равна нулю. Отсюда по доказанному выше 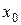- точка глобального минимума функции 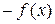, а стало быть 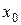- точка глобального максимума функции 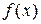на интервале .

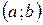Теоремы 16.1 и 16.2 выражают достаточные условия существования глобального экстремума для функции 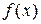на интервале. В основе решения задач на глобальный экстремум функции 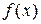на отрезке лежит теорема Вейерштрасса, согласно которой непрерывная на отрезке функция имеет на этом отрезке точки глобального минимума и максимума. Глобальный экстремум может достигаться либо внутри отрезка, либо на его концах. Если глобальный экстремум принимается во внутренней точке отрезка, то эта точка является и точкой локального экстремума, а следовательно, по теореме 15.1 и критической точкой функции. Отсюда, в случае конечного числа критических точек внутри отрезка, для отыскания глобального минимума (максимума) функции на отрезке следует вычислить значения функции в этих точках, а также на концах отрезка и выбрать среди них наименьшее (наибольшее).

Дата добавления: 2014-01-14